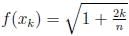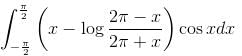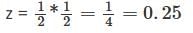GATE Mathematics Mock Test - 2 - GATE Mathematics MCQ
30 Questions MCQ Test GATE Mathematics Mock Tests - GATE Mathematics Mock Test - 2
The question given below consists of a pair of related words followed by four pain of words. Select the pair that best expresses the relation in the original pair.
LEGEND : MAP ::
Consider the differential equestion  and y = 0 and x → -∞ then
and y = 0 and x → -∞ then 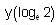 is
is
Convert Cartesian coordinates (2, 6, 9) to Cylindrical and Spherical Coordinates.
Let 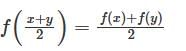 for all real x and y. If f’(0) exists and equals – 1 and f(0) = 1, then find f(2).
for all real x and y. If f’(0) exists and equals – 1 and f(0) = 1, then find f(2).
What is the number of subgroups of S4 of order 12 ?
If 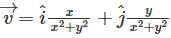 what is the value of this integral
what is the value of this integral 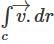 the circular path x2 + y2 = 1 ?
the circular path x2 + y2 = 1 ?
Let there be a vector X = yz2 ax + zx2 ay + xy2 az. Find X at P(3,6,9) in cylindrical coordinates.
In conics, the _____ is revolving to form two anti-parallel cones joined at the apex.
Given f (x) = ex cosy, what is the value of the fifth term in Taylor's series near (1, π/4) where it is expanded in increasing order of degree & by following algebraic identity rule?
In a Binomial Distribution, if p, q and n are probability of success, failure and number of trials respectively then variance is given by
Determine the logarithmic function of ln(1 + 5x)-5
Find the distance between two points A(5,60.,0) and B(10,90.,0) where the points are given in Cylindrical coordinates.
For a third degree monic polynomial, it is seen that the sum of roots are zero. What is the relation between the minimum angle to be rotated to have a Rolles point (α in Radians) and the cyclic sum of the roots taken two at a time c
If x3y2 is an integrating factor of (6y2 + axy)dx + (6xy + bx2)dy =0, a, b ∈ ℝ then
If f(x) = x3 + 3x2 + Sin(x) and g(x) = ex – 1 than find value of 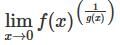
What is the formula used to find the area surrounded by the curves in the following diagram?
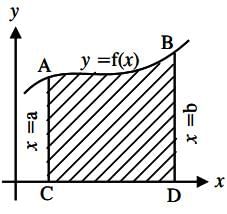
A Function f(x) has the property f(a) = f(b) for ∀a,b…∈….I and a + b = 20 then which of the following even degree polynomials could be f(x)
If f(x) = x2 – 3x + 2 and g(x) = x3 – x2 + x – 1 than find value of 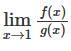
The graph of f(x) passes through the point (-1; 4). The slope of the line tangent to the graph at the point (x; f(x)) is -2x -3. Find f(0).
Find the limit of Riemann sums that is equal to the defnite integral 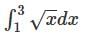
The extremium value of the function z = xy over the plane x + y = 1 is (upto two decimal places) _________.


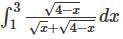
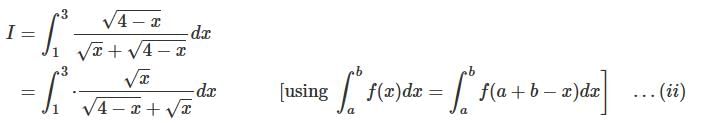
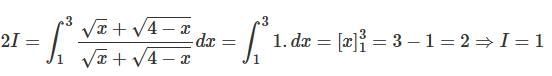

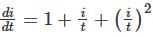 .
.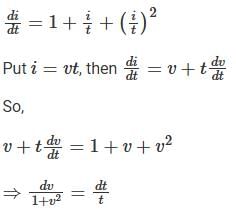
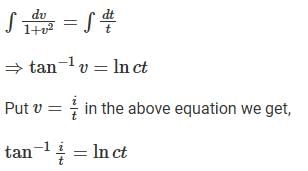
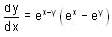
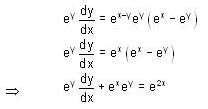
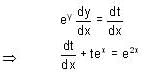
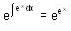
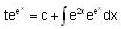
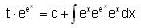
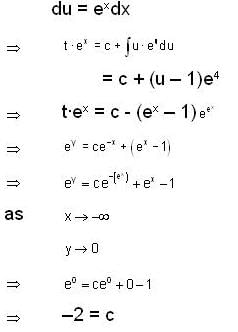
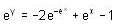
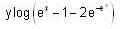
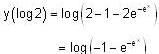
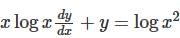 .
.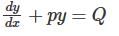
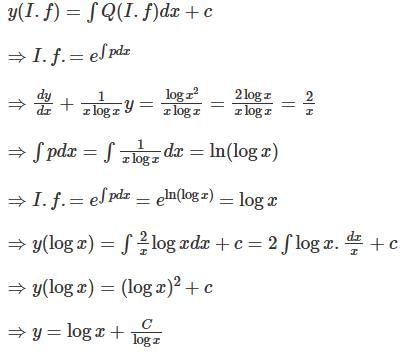
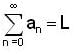 and if
and if 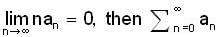 is
is
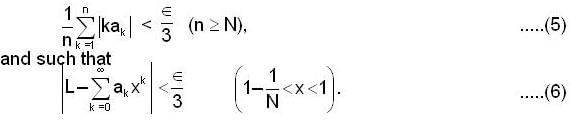
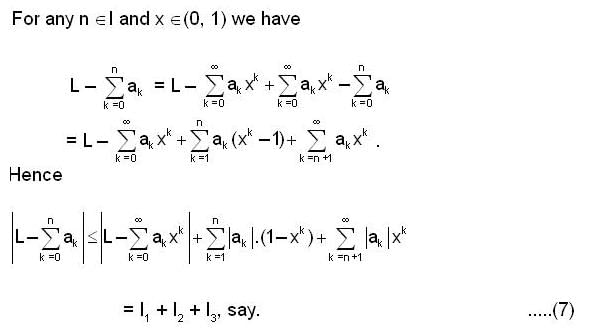
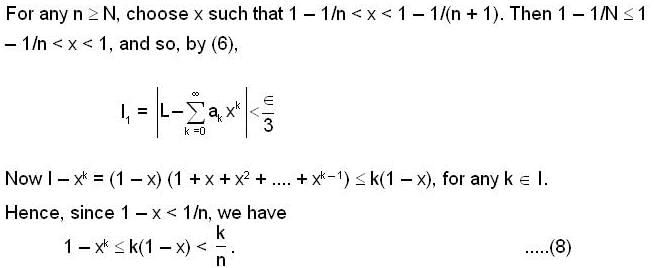
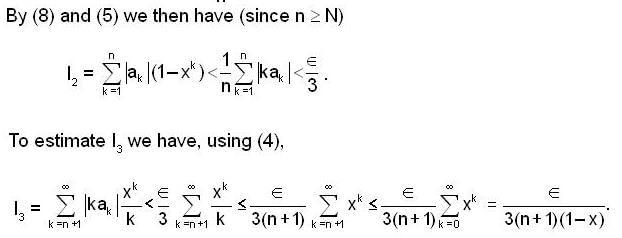
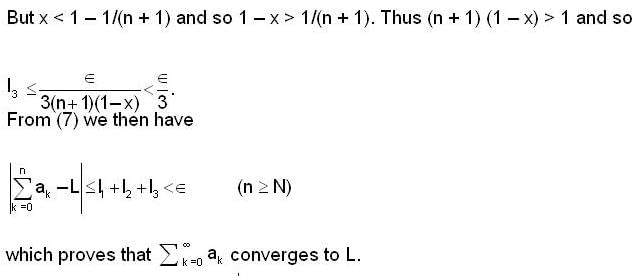
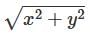 and
and 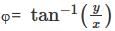 and z = z where (x, y, z) is the Cartesian coordinates. The Spherical coordinates is of the form (r, θ, φ) where
and z = z where (x, y, z) is the Cartesian coordinates. The Spherical coordinates is of the form (r, θ, φ) where 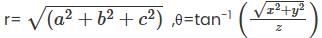 and
and  .Now, substituting the values for x as 2, y as 6 and z as 9, we get the answer as (6.32, 71.565., 9) and (11, 35.097., 71.565.).
.Now, substituting the values for x as 2, y as 6 and z as 9, we get the answer as (6.32, 71.565., 9) and (11, 35.097., 71.565.).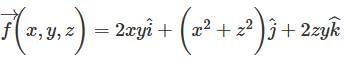 is
is
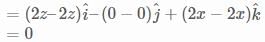
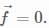
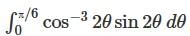 .
.
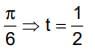
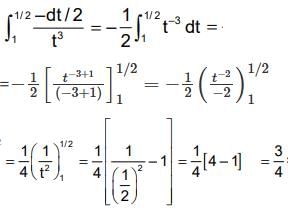
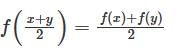
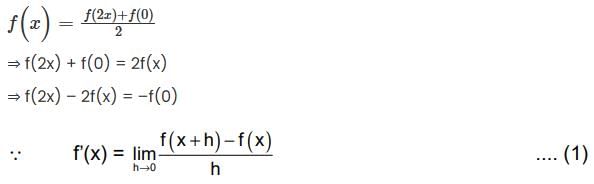

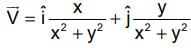
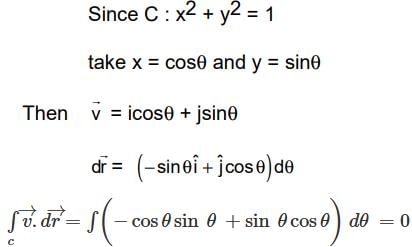
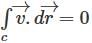 .
.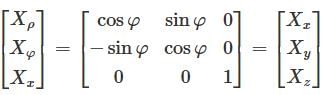
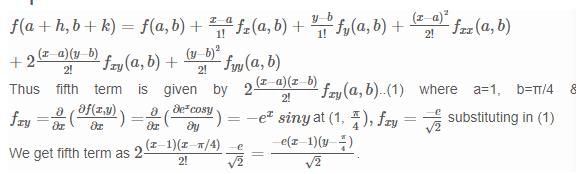
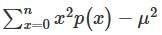
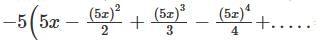
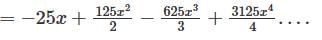
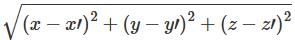 and substituting the values of x, y, and z in it, we get the required answer as 6.19 units. This sum can also be solved using a direct formula to find distance using two points in Cylindrical coordinates.
and substituting the values of x, y, and z in it, we get the required answer as 6.19 units. This sum can also be solved using a direct formula to find distance using two points in Cylindrical coordinates.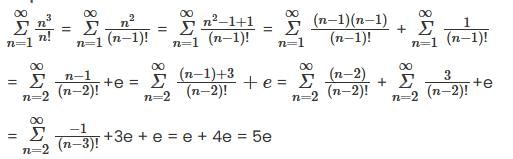
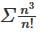 converges and sum is 5e.
converges and sum is 5e.

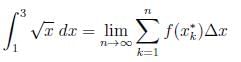
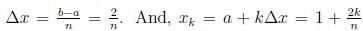 . Iff we let
. Iff we let 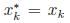 we have
we have