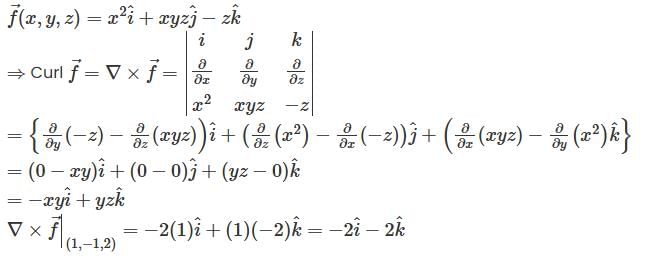IIT JAM Mathematics Mock Test- 2 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Mock Test- 2
The sections cut by a plane on a right circular cone are called as ______
In conics, the _____ is revolving to form two anti-parallel cones joined at the apex.
Computation of the discrete logarithm is the basis of the cryptographic system _______
For the function f(x) = x2 – 2x + 1
we have Rolles point at x = 1. The coordinate axes are then rotated by 45 degrees in anticlockwise sense. What is the position of new Rolles point with respect to the transformed coordinate axes
If the plane cuts at an angle to the axis but does not cut all the generators then what is the name of the conics formed?
If ‘p’, ‘q’ and ‘n’ are probability pf success, failure and number of trials respectively in a Binomial Distribution, what is its Standard Deviation ?
Convert the (10, 90, 60) coordinates to Cartesian coordinates which are in Spherical coordinates.
What is the divergence of the vector field 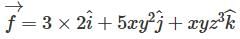 at the point (1, 2, 3).
at the point (1, 2, 3).
If ‘X’ is a random variable, taking values ‘x’, probability of success and failure being ‘p’ and ‘q’ respectively and ‘n’ trials being conducted, then what is the probability that ‘X’ takes values ‘x’? Use Binomial Distribution
While cutting, if the plane is at an angle and it cuts all the generators, then the conic formed is called as ______
In a Binomial Distribution, if p, q and n are probability of success, failure and number of trials respectively then variance is given by
What is the minimum angle by which the coordinate axes have to be rotated in anticlockwise sense (in Degrees), such that the function f(x) = 3x3 + 5x + 1016 has at least one Rolles point
Convert Cartesian coordinates (2, 6, 9) to Cylindrical and Spherical Coordinates.
Let there be a vector X = yz2 ax + zx2 ay + xy2 az. Find X at P(3,6,9) in cylindrical coordinates.
In a Binomial Distribution, if ‘n’ is the number of trials and ‘p’ is the probability of success, then the mean value is given by
It is suitable to use Binomial Distribution only for
For the function f(x) = x3 + x + 1
we do not have any Rolles point. The coordinate axes are transformed by rotating them by 60 degrees in anti-clockwise sense. The new Rolles point is
Find the distance between two points A(5,60.,0) and B(10,90.,0) where the points are given in Cylindrical coordinates.
For a third degree monic polynomial, it is seen that the sum of roots are zero. What is the relation between the minimum angle to be rotated to have a Rolles point (α in Radians) and the cyclic sum of the roots taken two at a time c
Convert the vector P to Cartesian coordinates where P = r ar + cosθ aφ.
Determine the logarithmic function of ln(1 + 5x)-5
For the infinitely defined discontinuous function
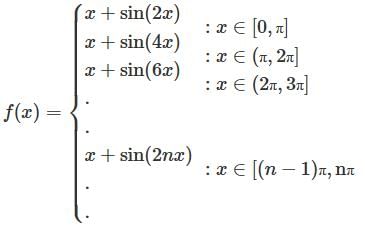
How many points 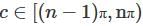 such that
such that




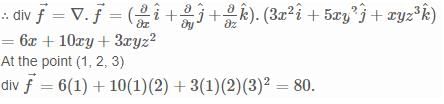
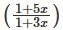
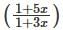
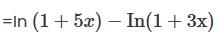
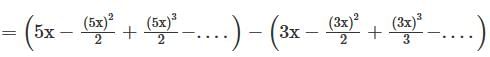
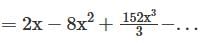
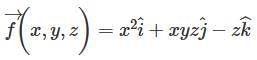 at the point (2, 1, -2).
at the point (2, 1, -2).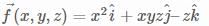
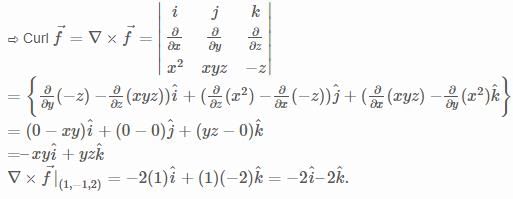

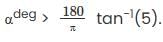
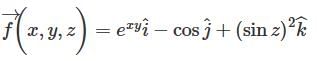
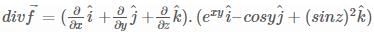
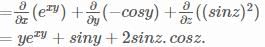
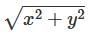 and
and 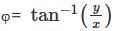 and z = z where (x, y, z) is the Cartesian coordinates. The Spherical coordinates is of the form (r, θ, φ) where
and z = z where (x, y, z) is the Cartesian coordinates. The Spherical coordinates is of the form (r, θ, φ) where 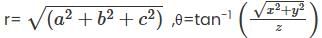 and
and  .Now, substituting the values for x as 2, y as 6 and z as 9, we get the answer as (6.32, 71.565., 9) and (11, 35.097., 71.565.).
.Now, substituting the values for x as 2, y as 6 and z as 9, we get the answer as (6.32, 71.565., 9) and (11, 35.097., 71.565.).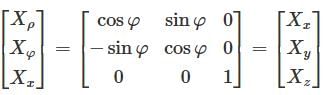
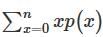
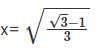
 and substituting the values of x, y, and z in it, we get the required answer as 6.19 units. This sum can also be solved using a direct formula to find distance using two points in Cylindrical coordinates.
and substituting the values of x, y, and z in it, we get the required answer as 6.19 units. This sum can also be solved using a direct formula to find distance using two points in Cylindrical coordinates.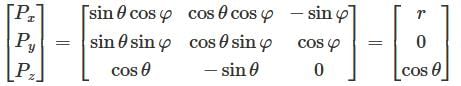
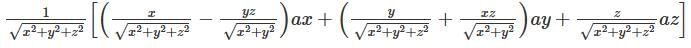
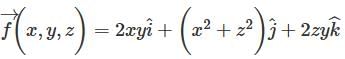 is
is
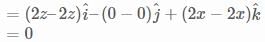

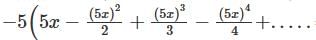
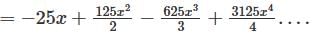
 at the point (2,1,-2).
at the point (2,1,-2).