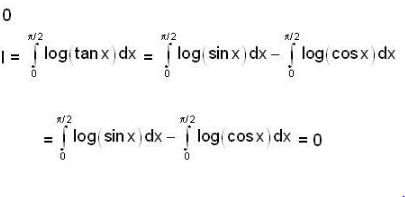IIT JAM Mathematics Practice Test- 12 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 12
The subset 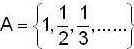 of R has limit point and isolated points respectively as.
of R has limit point and isolated points respectively as.
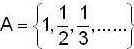 of R has limit point and isolated points respectively as.
of R has limit point and isolated points respectively as.A sequence {xn} is defined by 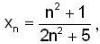 then find a positive integer m such that Lim xn = 1/2.
then find a positive integer m such that Lim xn = 1/2.
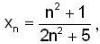 then find a positive integer m such that Lim xn = 1/2.
then find a positive integer m such that Lim xn = 1/2.If <Sn> be a convergent sequence of positive numbers such that 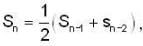 for all n ≤ 2; then lim Sn is
for all n ≤ 2; then lim Sn is
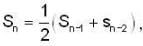 for all n ≤ 2; then lim Sn is
for all n ≤ 2; then lim Sn isLet {an} be a sequence of positive numbers. Then
A real number P is said to be a cluster point of a sequence <an> if to each ε >0 and each positive integer m, there exists a positive integer m0 > m such that
Let {an} be a sequence of non-negative real n o s such that the series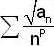 ,is convergent. If P is a real number such that the series
,is convergent. If P is a real number such that the series 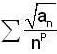 diverges, then
diverges, then
If each value of a series is multiplied by 2, then radius of convergence of the reslting series is,
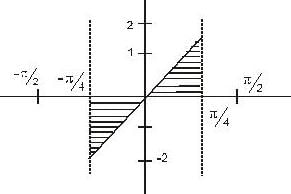
The volume of the solid generated by revolving about the x-axis the region bounded by y = 2 tan x, y = 0, x 
The Surface Area of the cone z2 = x2 + y2 which lies inside the cylinder x2 + y2 = 2x, is
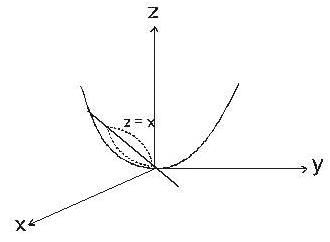
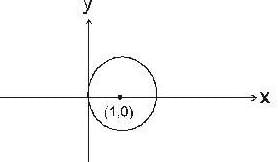
The volume of the solid which is bounded by the surfaces 2z = x2 +y2 and z = x is,
The volume of the solid which is below thee plane z =2x + 3 and above the xy-plane and bounded by y2 = x = 0 and x = 2, is given by,
If for a real y, {y} is the greatest integer less than or equal to y, then the value of the integral 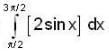 is
is
A function, f(x) = 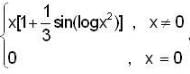 where {.} be greatest integer function, then
where {.} be greatest integer function, then
If x1, x2 are positive and 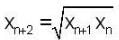 , then which of the following statement(s) is/are correct, if we take x1 > x2?
, then which of the following statement(s) is/are correct, if we take x1 > x2?
If u1 and v1 are given unequal real no.'s and 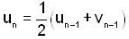 and
and 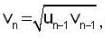 where n ≥ 2, then
where n ≥ 2, then
Consider the seqn {xn}, where x1 = √7 and xn+1 = 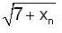 , n ≥ 1 then
, n ≥ 1 then
Consider the seqn {sn} where sn = sin(nπθ), where θ be a rational no. such that 0 < θ < 1, then,
If sequence {xn} where x1 = 1, 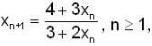 then its limit is_____.
then its limit is_____.
Let a = min {x2+2x+3 ; x ∈ R} and b = 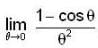 , then the value of
, then the value of 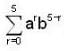 is _______.
is _______.
The radius of convergence of the power Series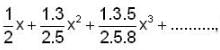 is ______.
is ______.
Let {an} be a sequence of real no's where  is equal to _____.
is equal to _____.
The maximum value of the function f(x,y) = 3x + 4y on the circle x2 +y2 = 1
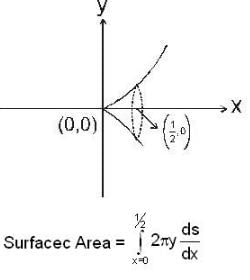
If the Area of the surface generated by revolving the curve y = x3, 0 ≤ x ≤ 1/2, about the x-axis is kπ/1728 then k is equal to .....
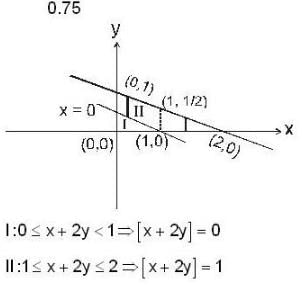
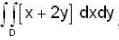 , where [x] is greatest integer less than or equal to x and D is the region bounded by x = 0, y = 0 and x + 2y = 2, then the value of givin integral is .....
, where [x] is greatest integer less than or equal to x and D is the region bounded by x = 0, y = 0 and x + 2y = 2, then the value of givin integral is .....


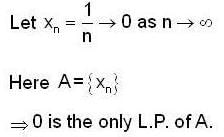
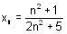
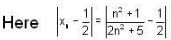
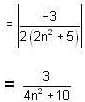
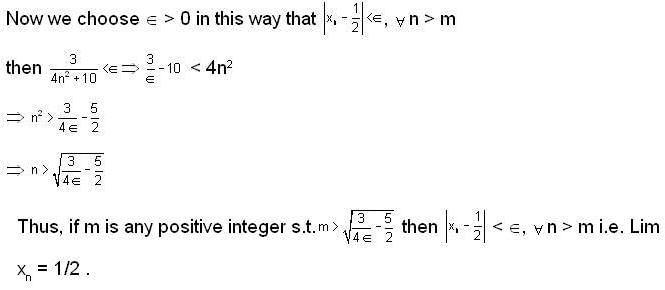

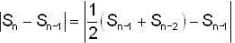
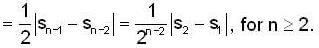 .....(i)
.....(i)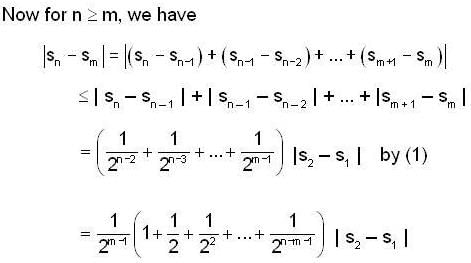
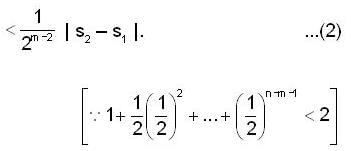



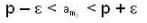
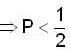
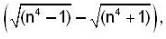 is
is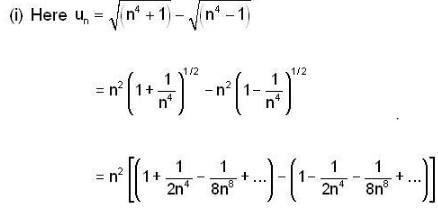

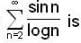


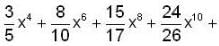 ....... is
....... is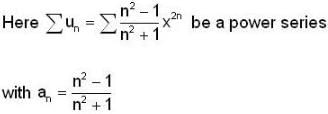
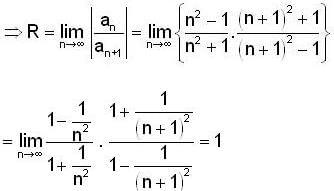

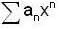
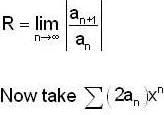

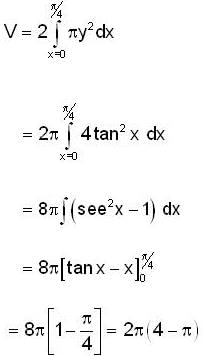
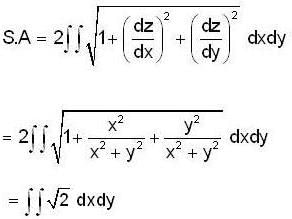
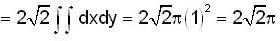
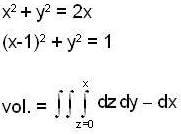
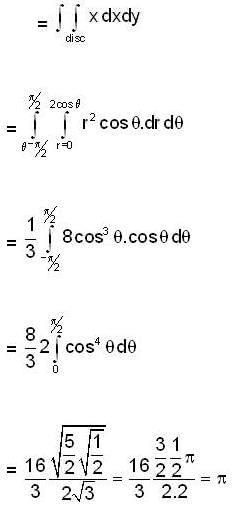
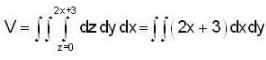
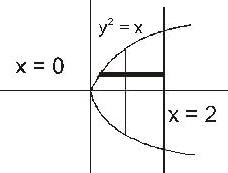
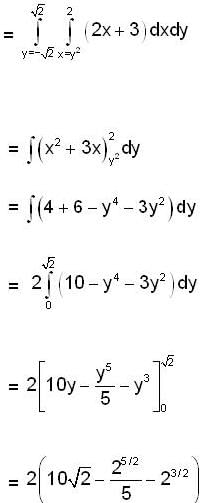
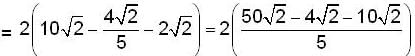
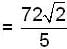
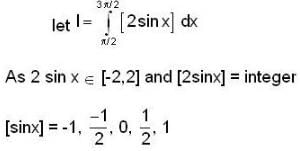
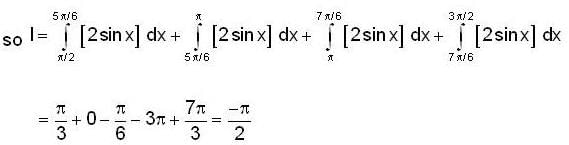
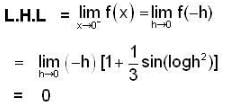

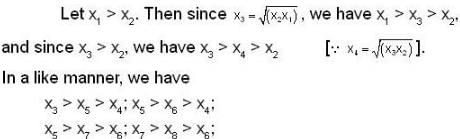
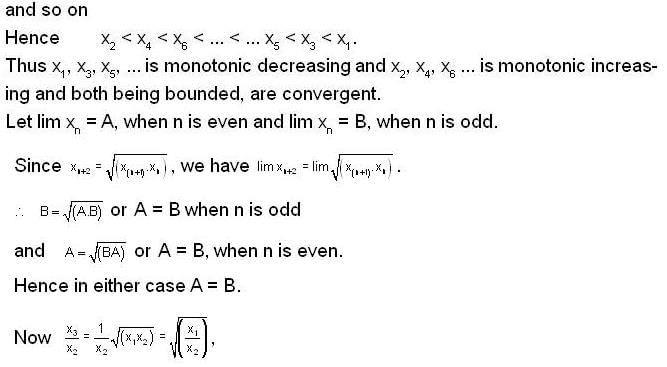
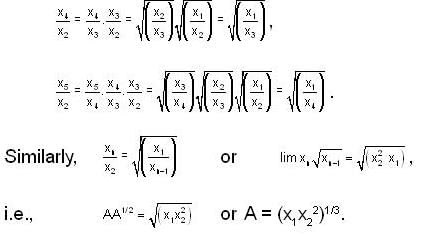
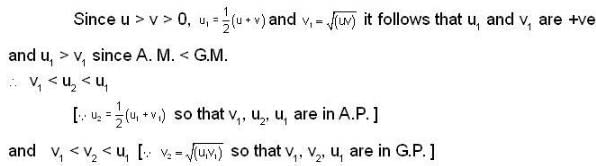

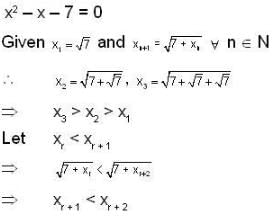

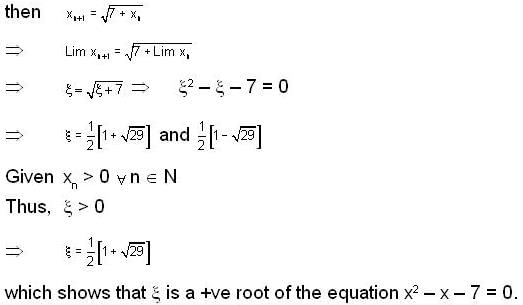

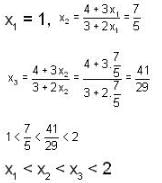
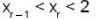
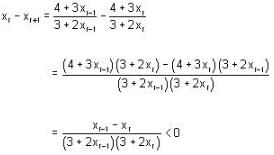

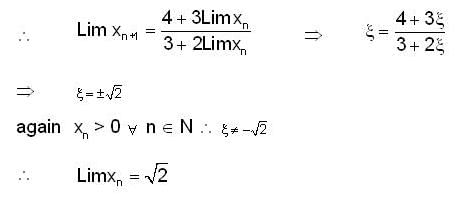
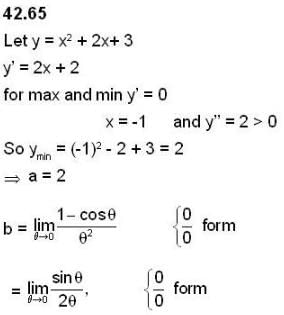
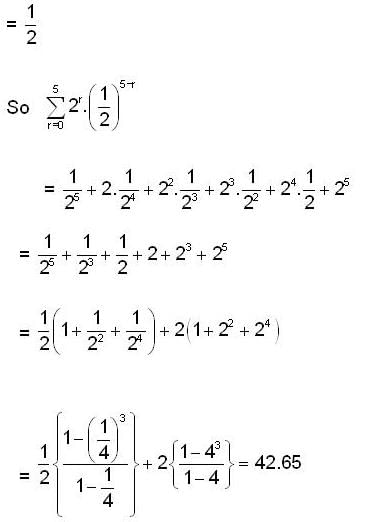
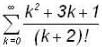 converge to ______.
converge to ______.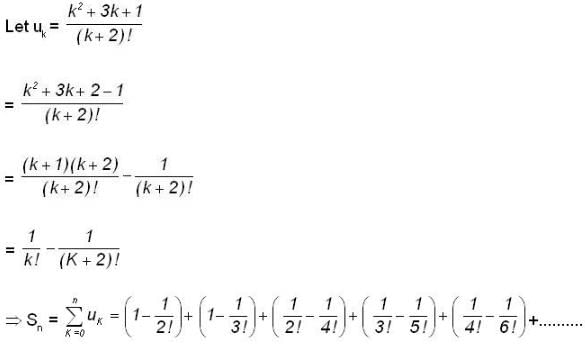
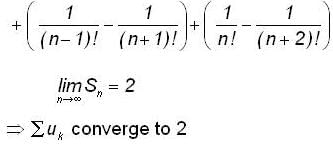
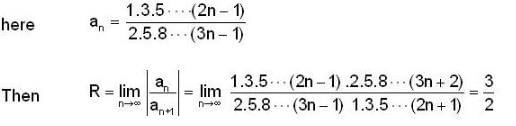
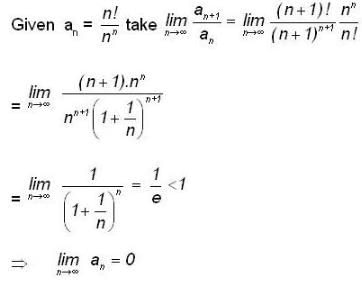
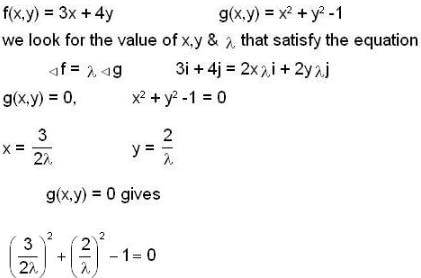
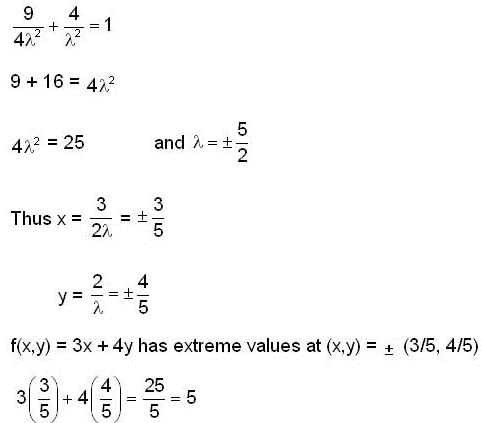
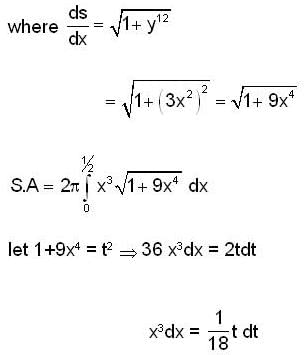
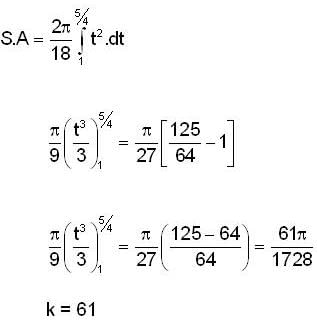
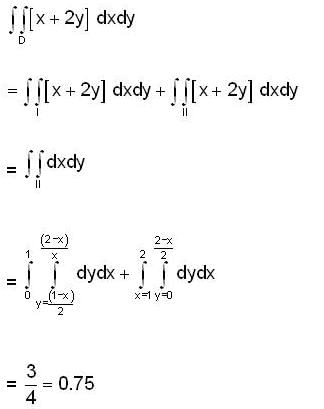
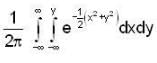 is equal to ....
is equal to ....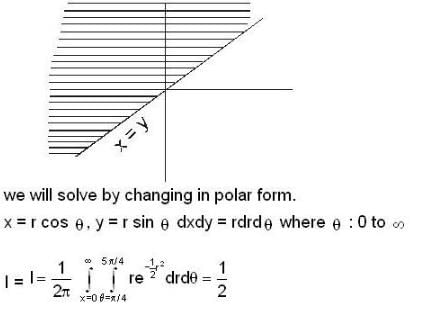
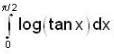 is ......
is ......