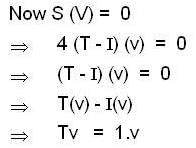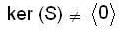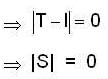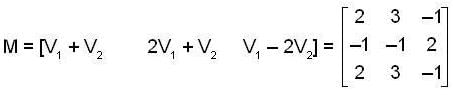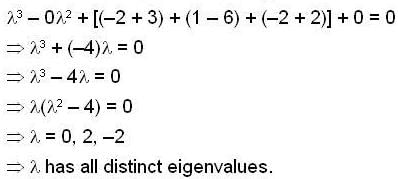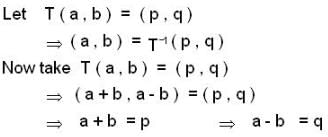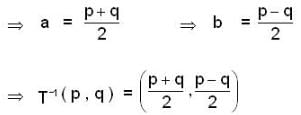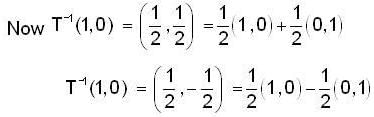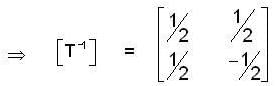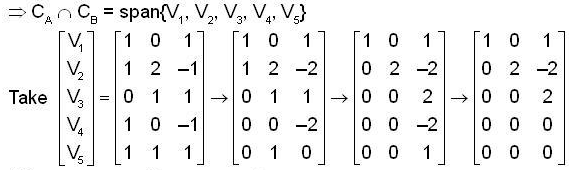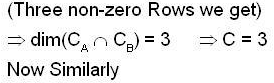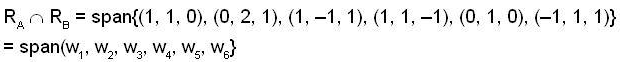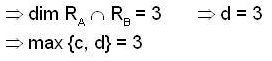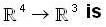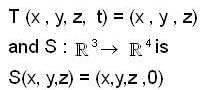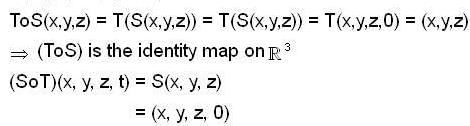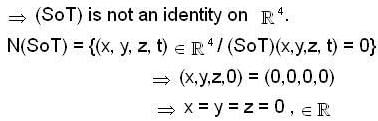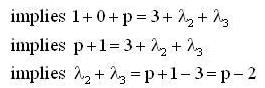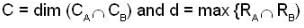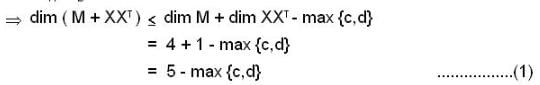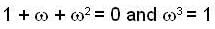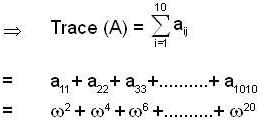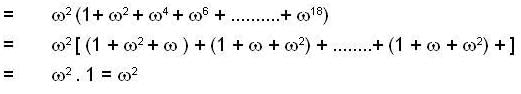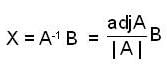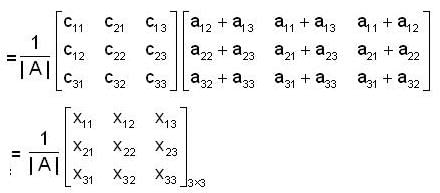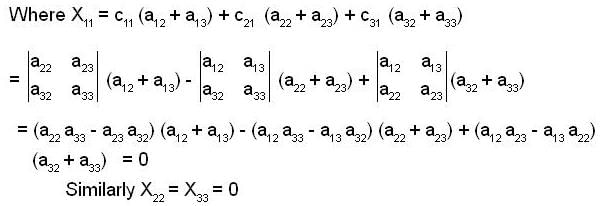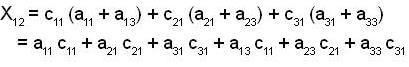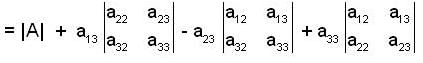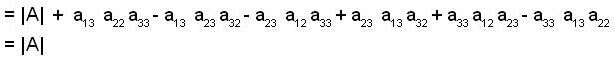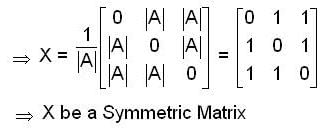IIT JAM Mathematics Practice Test- 15 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 15
If 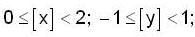 and
and 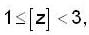 where [ . ] be the greatest integer function, then the maximum value of the determinant
where [ . ] be the greatest integer function, then the maximum value of the determinant 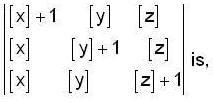
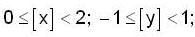 and
and 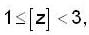 where [ . ] be the greatest integer function, then the maximum value of the determinant
where [ . ] be the greatest integer function, then the maximum value of the determinant 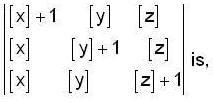
Let V be a 3 dimensional vector space with A and B its subspaces of dimensions 2 and 1 , respectively. If 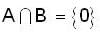 , then
, then
The rank of the following ( n + 1 ) x ( n + 1 ) matrix , were a is real no.

Let A, B be n x n matrices such that BA+ B2 = I - BA2, where I is the nxn identity matrix, which of the following is always true ?
The determinant of the n x n permutation matrix

(where [x] be greatest integer not exceeding x)
Which of the following sets is a basis for the subspace 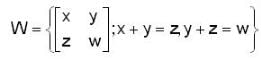 of fhe vector o f all 2 x 2 real matrices over R ?
of fhe vector o f all 2 x 2 real matrices over R ?
Let a, b, c and d are the eigenvalues of the matrix

The a2 + b2 + c2 + d2 is equal to?
Consider the following two statements
(I) If V be a vector space over F of dimension 5 and U and W are subspaces of V of dimension 3. Then 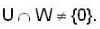
(II) Let V be the set of all polynomials over Q of degree 2 together with the zero polynomial. Then V be a vector space over Q.
Then which of the above statement’s are correct?
Let  are two vector spaces over R, then which of the following subset’s is a subspace?
are two vector spaces over R, then which of the following subset’s is a subspace?
Let A be a 3 x 3 matrix with eigen values 1 , - 1 , 0 . then the determinant of 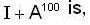
Let V be the vector space of all real polynomials. Consider the subspace W spanned by t2 + t +2, t2 +2t +5, 5t2 +3t + 4, and 2t2 +2t+ 4. Then the dimension of W is,
Let T be a Linear Transformation from 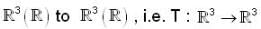 be a Linear Transform ation defined by T (a ,b ,c ) = ( 3a , a - b , 2a + b + c ) , then T-1 (1,2,3) is
be a Linear Transform ation defined by T (a ,b ,c ) = ( 3a , a - b , 2a + b + c ) , then T-1 (1,2,3) is
The linear Transformation  , whose image is generated by {(1,2,0,-4), (2,0,-1,-3)} is,
, whose image is generated by {(1,2,0,-4), (2,0,-1,-3)} is,
Let P4 denote the real vector space of all polynomials with real coefficients of degree at most 4. Consider the map T : P4 → P4 given by T[P(x)] = P"(x) + P'(x) + P(x). Then,
Let T be a linear operator on R3 (R), defined by,
T(a , b, c) = ( 3a , a - b , 2a+ b + c ) , then (T2 — I )(T — 3I) is,
(where I be a linear operator on R3)
Let 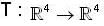 be a linear transform ation satisfying T3 + 3T2 = 4I, where I is the identity transformation. Then the linear transformation S = T4 + 3T3 - 4I is
be a linear transform ation satisfying T3 + 3T2 = 4I, where I is the identity transformation. Then the linear transformation S = T4 + 3T3 - 4I is
Let  Let M be the matrix whose columns are, V1+V2, 2V1 + V2, V1 - 2V2 in that order. Then which of the followings is not true for Matrix M ?
Let M be the matrix whose columns are, V1+V2, 2V1 + V2, V1 - 2V2 in that order. Then which of the followings is not true for Matrix M ?
Define 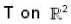 into itself by,
into itself by, 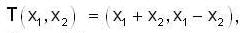 Then, matrix of T-1 relative to the standard basis for
Then, matrix of T-1 relative to the standard basis for 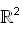 is
is
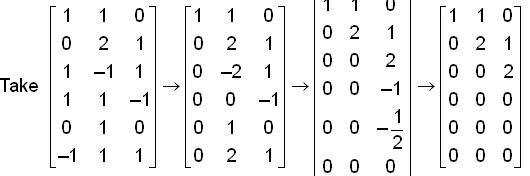
Let A and B are two 3 * 3 real matrices. Let CA and CB denotes the span of the columns of A and B respectively and RA, RB denotes the span of the rows of A and B respectively.
where

Then the max {c, d}, where 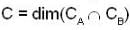 and
and 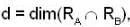 is given by,
is given by,
Let  be linear transformation such that ToS is the identity map on
be linear transformation such that ToS is the identity map on 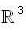 , Then
, Then
The matrix 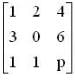 has one eigen value equal to 3. The sum of the other two eigen values is
has one eigen value equal to 3. The sum of the other two eigen values is
Let M be a 7 x 7 matrix of Rank 4 with real entries, let 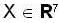 be a column vector. Then Rank of M + XX7 is at least
be a column vector. Then Rank of M + XX7 is at least
Let A be a 10x10 real matrix, whose elements are defined as 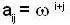 (where w is cube root of unity), Then trace of A is ,
(where w is cube root of unity), Then trace of A is ,
let A = [ aij] be a 3x3 invertible matrix with real entries and B = [bij] be a matrix which is formed such that bij is the sum of all the elements except aij in the ith row. Answer the following:
If there exist a matrix X with Constant elements such that A X = B, then X is
Let M be a m X n (m < n) matrix with rank m. Then


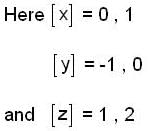
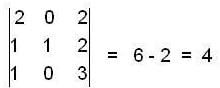
 and
and 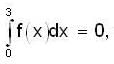 then a is equal to
then a is equal to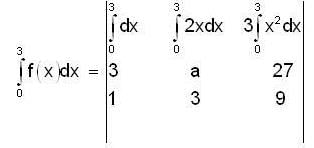

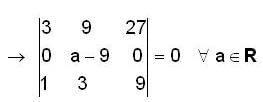
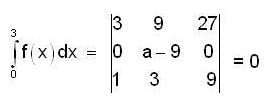

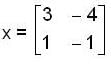 , then the value of xn is ,
, then the value of xn is ,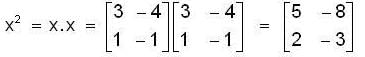
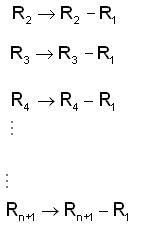

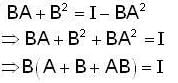
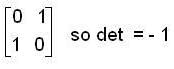
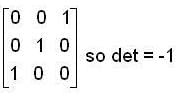

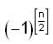
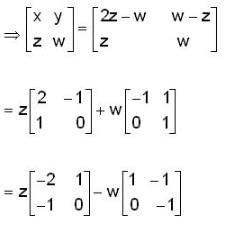

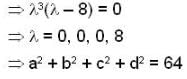
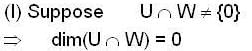
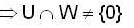
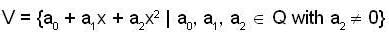 and F = Q
and F = Q

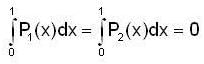
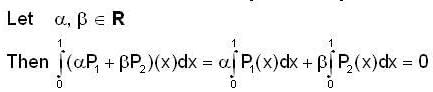
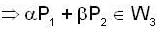
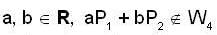
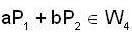
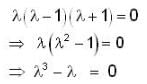
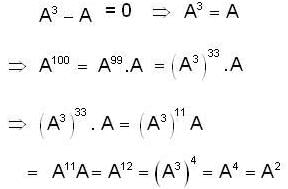
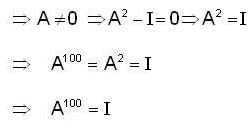 so
so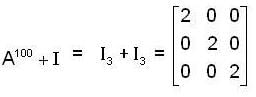

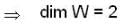
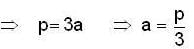
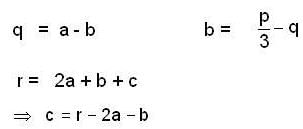
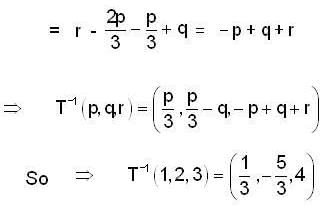

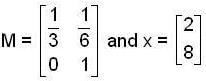 then
then 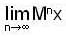 is
is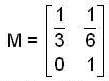
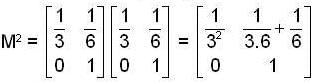
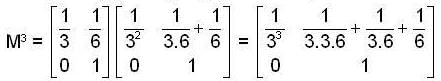
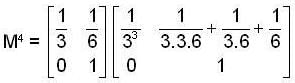

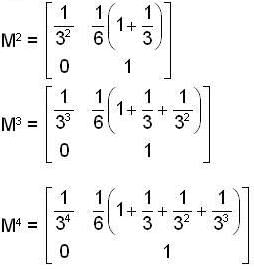
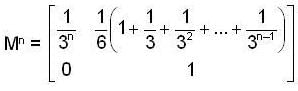

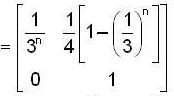
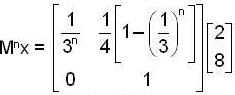
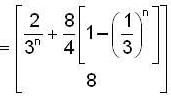
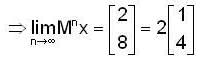
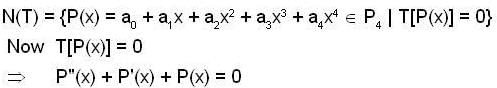
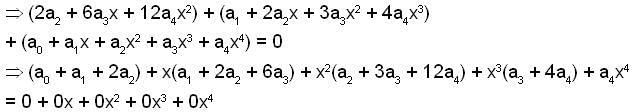
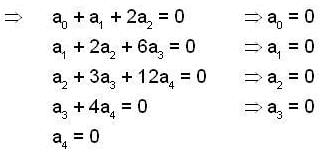
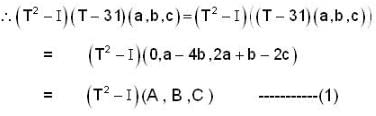
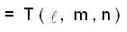
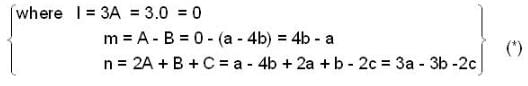
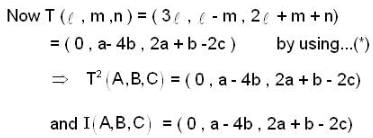
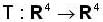 be a linear transformation,
be a linear transformation,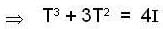 , is also a linear transformation, on
, is also a linear transformation, on