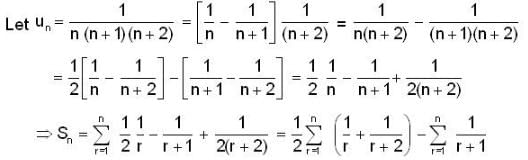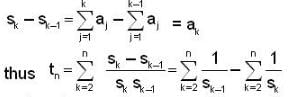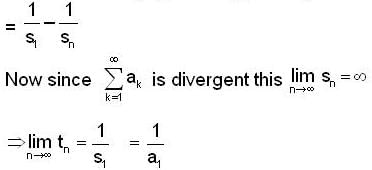IIT JAM Mathematics Practice Test- 18 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 18
Let [x] denote the greatest integer function of x. The value of α for which the function 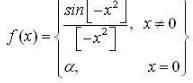 is continuous at x = 0 is
is continuous at x = 0 is
 is continuous at x = 0 is
is continuous at x = 0 is Let {an}, {bn} and {cn} be sequences of real numbers such that bn = a2n and cn = a2n+1. Then {an} is convergent
If {xn} is a sequence of real no.'s, then match list I with list II and select the correct answer using codes given below the list,


For what value of x, the infinite series, 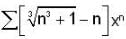 converges?
converges?
{an} is a sequence of real no.'s satisfying 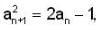 then
then
The radius of convergence of the power series ∑ ansn where 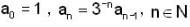 is
is
If f(x) = 3x - 2 and (gof)-1 (x) = x - 2, then function g(x) is
Let f : R → R be a differentiable function such that f(e) = e and 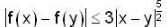 for all x ∈ R and y ∈ R. Let g(x) = logx f(x) for all x > 0, then g'(e) is equal to
for all x ∈ R and y ∈ R. Let g(x) = logx f(x) for all x > 0, then g'(e) is equal to
Which of the following is convergent series?
The internal of convergence of the power series,
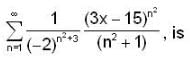
Let F : R → R be a differentiable function such that 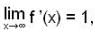 then
then
Let f : (-1, 1) → 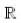 be defined as f(x) =
be defined as f(x) = 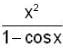 for x ≠ 0 and f(0) = 2.
for x ≠ 0 and f(0) = 2.
If f(x) = 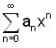 is the Taylor's expressing of f for all x in (-1,1) then
is the Taylor's expressing of f for all x in (-1,1) then 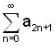 is,
is,
If f(x) = (x2-1) |x2-3x+2| + cos (|x|), then set of points of non-differentiability is
A function f : R → R, defined by f(x) = 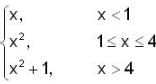
If T = {f(x) ; x ∈ R}, then the inverse function 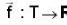
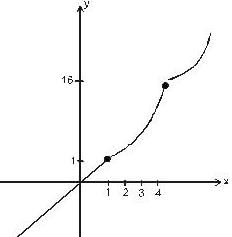
For which region, the series 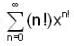 is convergent?
is convergent?
If f(x) = (x2-4) | x3 -6x2 + 11x - 6| + 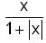 then the set of point at which the function f(x) is not differentiable is,
then the set of point at which the function f(x) is not differentiable is,
Let A be a proper subset of R, given as 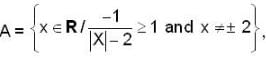 Then which of the following is true for A?
Then which of the following is true for A?
Let {an} be a sequence of real number's defined as 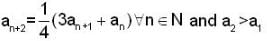 If{an} is convergent then it converge to
If{an} is convergent then it converge to
Let {an} be a sequence of real numbers with a1 > 0, a2 > 0 and 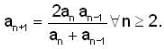 If a1 = 1 and a2 = 2 then the sequence {an} converge to?
If a1 = 1 and a2 = 2 then the sequence {an} converge to?
Let {an} be an increasing seqn of positive real numbers such that the series 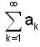 is divergent. Let
is divergent. Let  ... then
... then 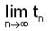 is equal to
is equal to


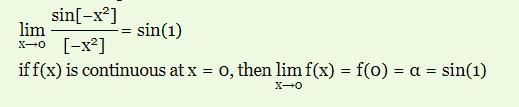

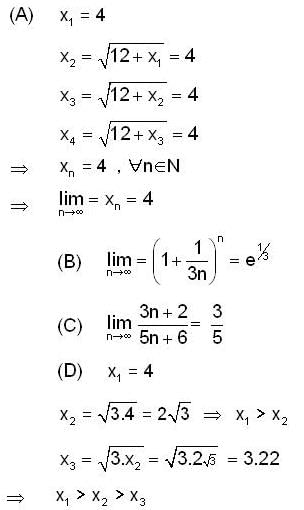

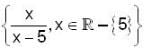 , then
, then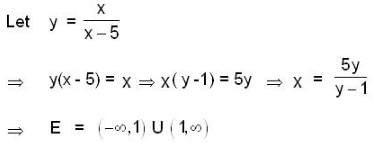
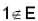 and also E is not bounded.
and also E is not bounded.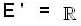


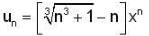
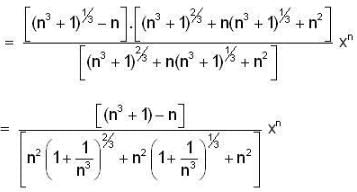

 then
then
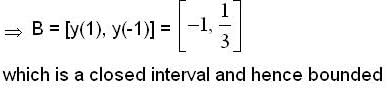
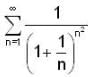 is,
is,
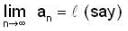
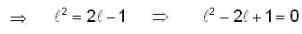
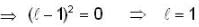
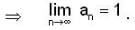
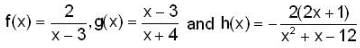 then
then 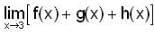 is,
is,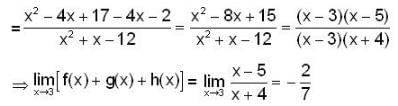
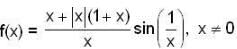
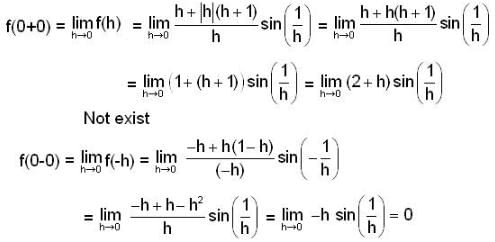
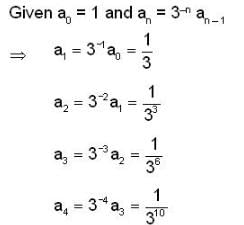
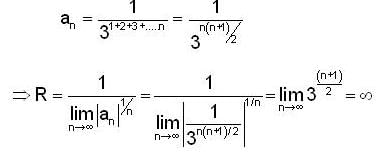
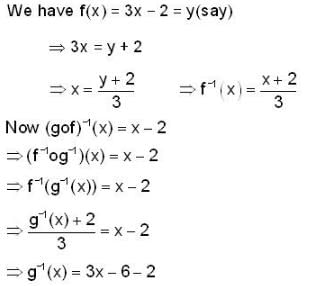
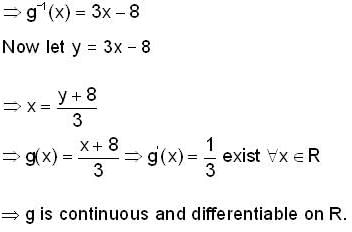
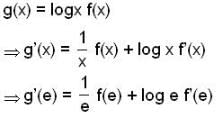
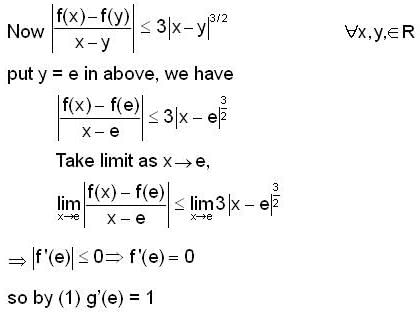
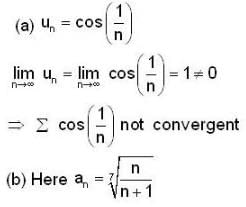

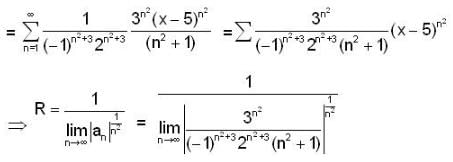
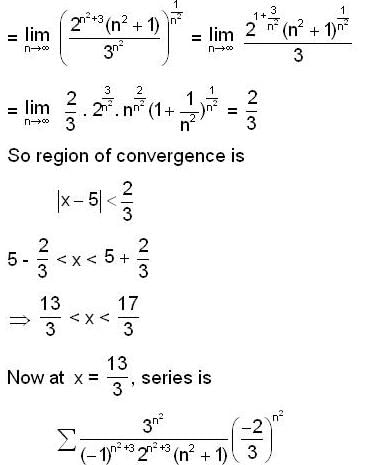
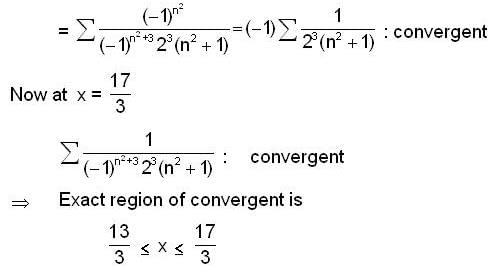


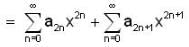 ...(1)
...(1)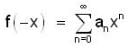
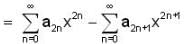 ...(2)
...(2)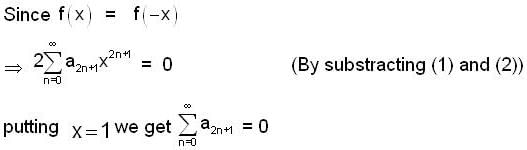
 converges if,
converges if,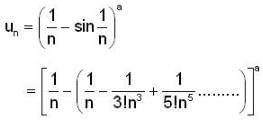

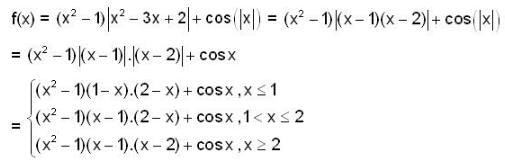
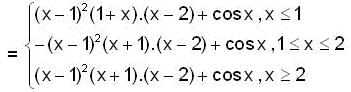
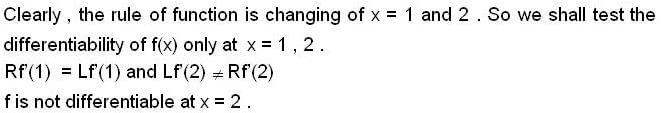

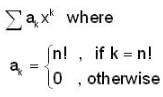
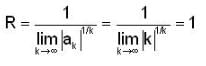
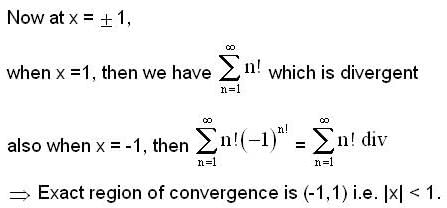


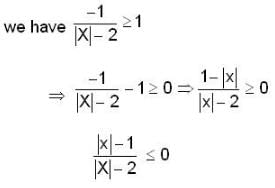

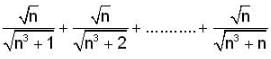 converges to,
converges to,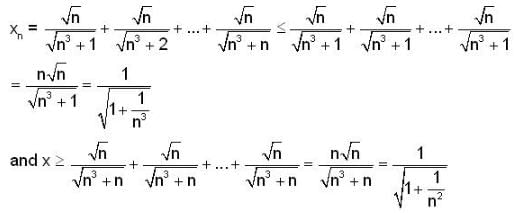

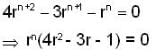
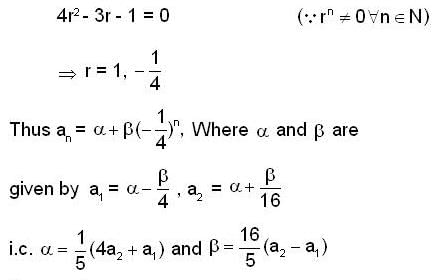
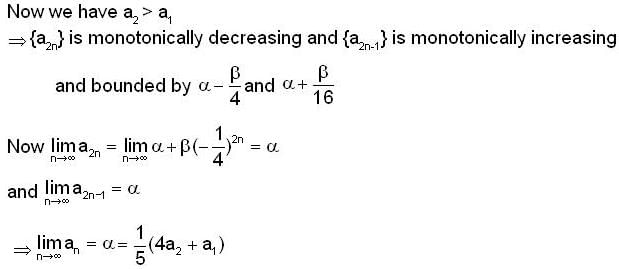
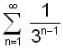 is :
is :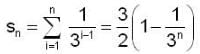
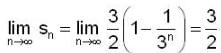
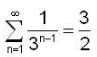

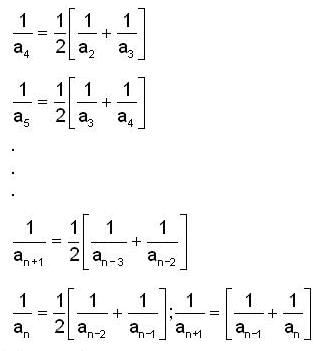

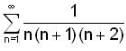 is
is