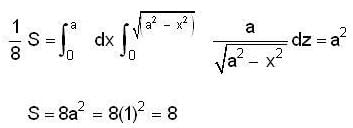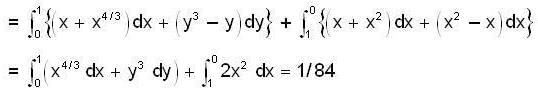IIT JAM Mathematics Practice Test- 3 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 3
Let f : R →R and g : R → R be continuous functions, then the value of the integral 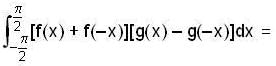
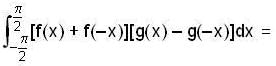
Let f : (0,∞) -> R and F(x) =  If F(x2) = x2(1 + x), then f(4) equals
If F(x2) = x2(1 + x), then f(4) equals
Let 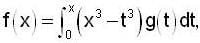 where g is a real-valued continuous function on R.
where g is a real-valued continuous function on R.
Then f'(x) is equal to
Let f : R → R be a continuous function. if 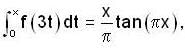 fo r all x ∈ R, then f(3) is equal to
fo r all x ∈ R, then f(3) is equal to
If a function f is continuous for x ≥ 0 and satisfies  then the value of f'(π/4) is -
then the value of f'(π/4) is -
Let f : R → R be a continuous function. If  for all x ∈ R , then f ( - 5 ) is equal to
for all x ∈ R , then f ( - 5 ) is equal to
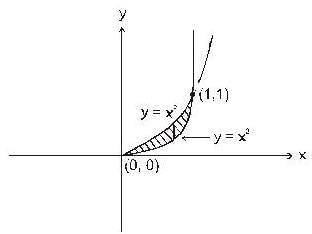
Evaluate 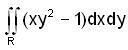 , where R is bounded by = x2 and y = x3
, where R is bounded by = x2 and y = x3
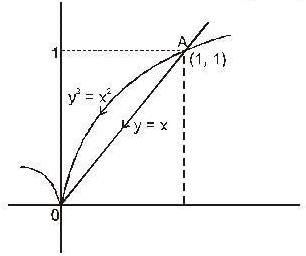
Find the length of the arc of the semi cubical parabola ay2 = x3 from its vertex to the point (a, a).
Evaluate the line integral 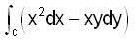 taken along the line segment from (1.0) to (0. 1)
taken along the line segment from (1.0) to (0. 1)
if 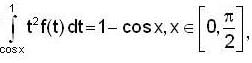 hen which of one of the following is/are not correct ?
hen which of one of the following is/are not correct ?
if 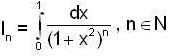 then which of the following statements are true?
then which of the following statements are true?
let f ; R — > R be a function with continuous derivative such that f(1) = 1.
if 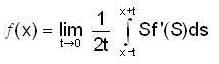 for all x ∈ R then,
for all x ∈ R then,
Let f : R -> R be a differentiable function having 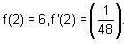 Then
Then 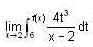 is equal to _____________.
is equal to _____________.
How many points of extrem um of the following integral 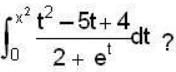
Let f : R → R be defined as
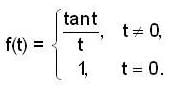
Then the value of 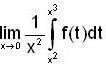 is equal to __________.
is equal to __________.
If f(x) is defined [-2, 2] by f(x) = 4x2 - 3x + 1 and 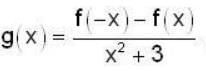 , then find the value of the integral
, then find the value of the integral 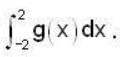
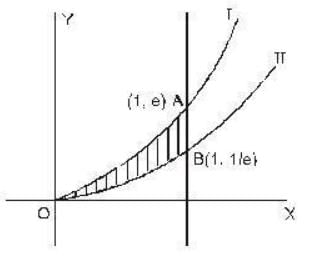
The area between the curves y = xex and y = xe-x and the line x = 1 is __________ ( Write upto Four decimal Places)
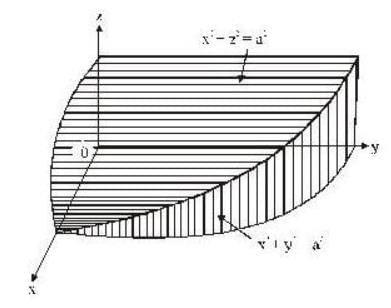
if a = 1 .then find the area of that part of the surface of the cylinder x2 + y2 = a2 which is cut only by the cylinder x2 + z2 = a2.
Find the value of 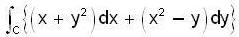 taken in the clockwise sense along the closed curve C formed by y3 = x2 and the chord joining (0, 0) and (1,1).
taken in the clockwise sense along the closed curve C formed by y3 = x2 and the chord joining (0, 0) and (1,1).


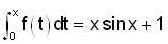 then
then  is
is
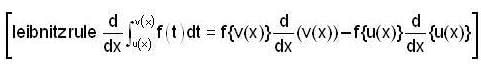 we get
we get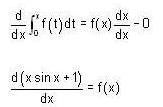
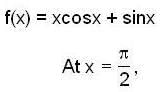
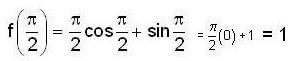
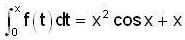 then f(0) is
then f(0) is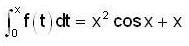 ..(1)
..(1)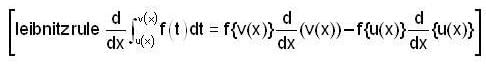
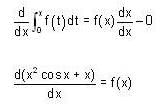

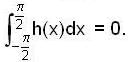

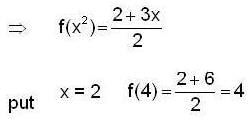
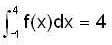 and
and 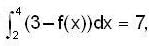 then the value of
then the value of 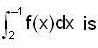
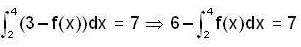
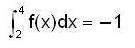
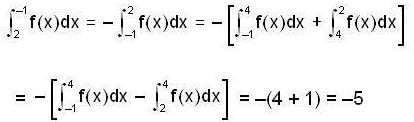
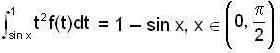 then
then 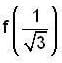 equal to
equal to 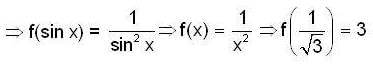
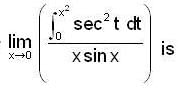
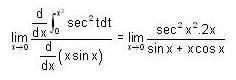
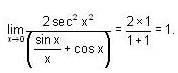
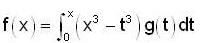
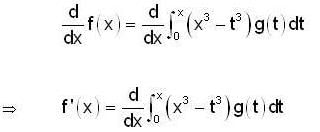
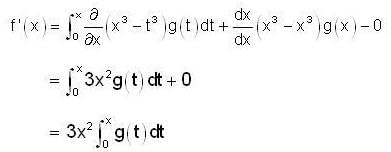
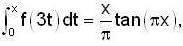
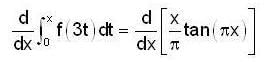
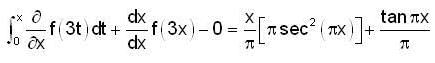
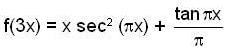
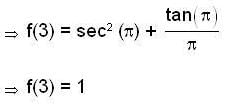
 = 2x + xcos2x.2+sin2x-sin2x
= 2x + xcos2x.2+sin2x-sin2x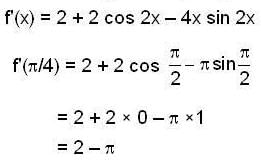

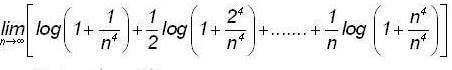
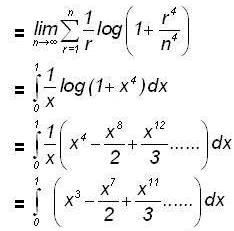
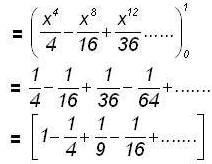
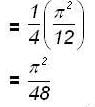
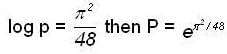
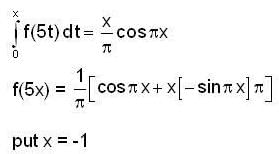


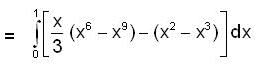

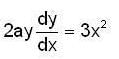
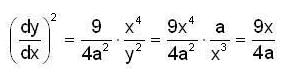 Therefore the required length
Therefore the required length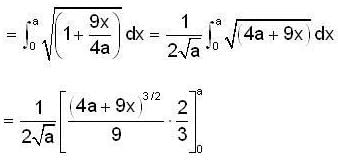
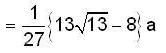
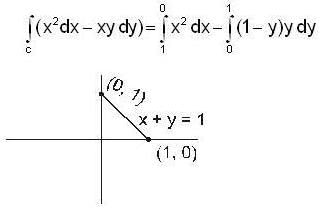
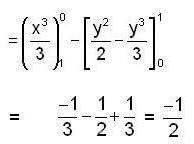
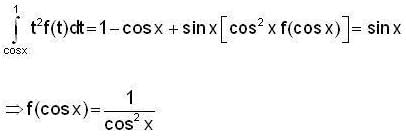


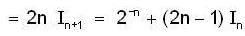
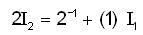
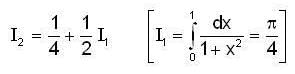
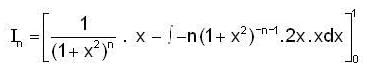
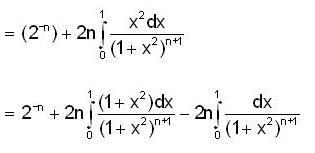
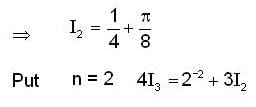
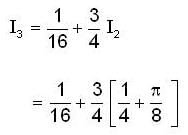
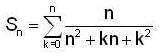 and
and 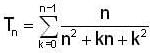 for n=1,2,3 .......... then
for n=1,2,3 .......... then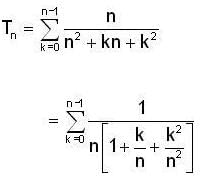
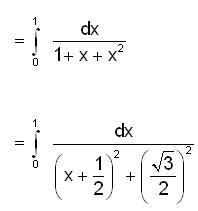
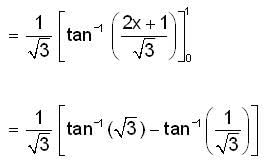
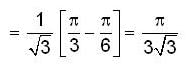
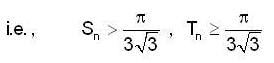
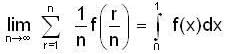 then
then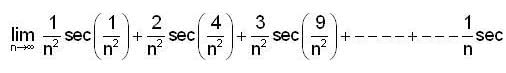 (1) is equal
(1) is equal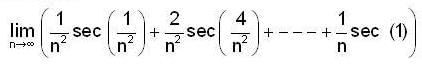


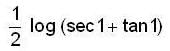
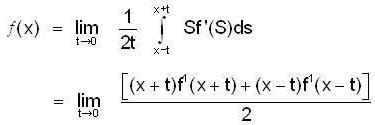
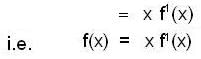
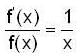
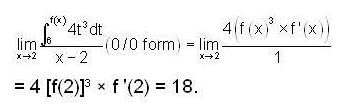
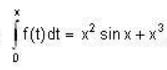 then
then 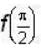 = _____ Write upto 4 decimal places
= _____ Write upto 4 decimal places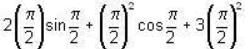
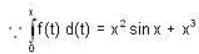
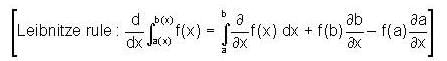
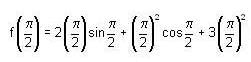
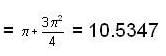
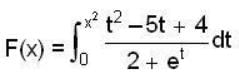
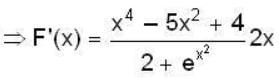
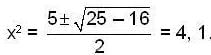
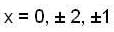
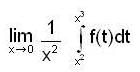
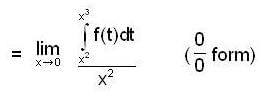
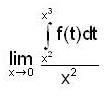
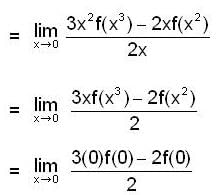
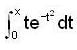 is __________.
is __________.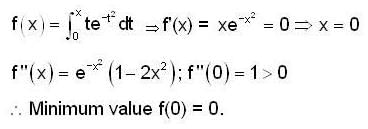
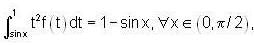 then
then 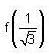 is _________.
is _________.

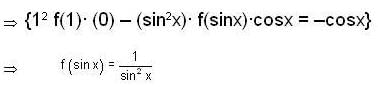
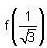 is obtained when
is obtained when 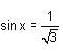
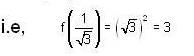
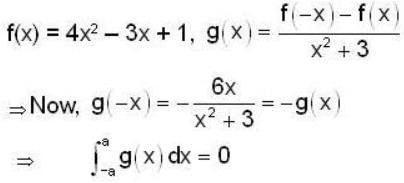

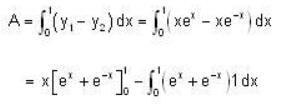
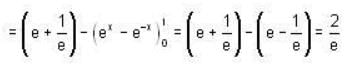
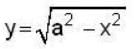
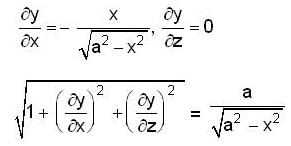
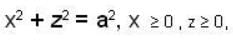 on the xz- plane, Thus, we have
on the xz- plane, Thus, we have