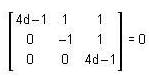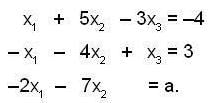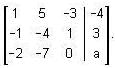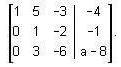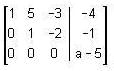IIT JAM Mathematics Practice Test- 5 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 5
If A is a non-zero column matrix of order m * 1 and B is a non-zero row matrix of order 1 * n, then rank of AB is equal to
If a 3 x 3 matrix A has its inverse equal to A, then A2 is equal to , ......
The sum of the eigen values of the matrix 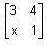 for real and negative values of x is
for real and negative values of x is
Let U be a 3 * 3 complex Hermitian matrix which is unitary. Then the distinct eigen values of U are
Let the characteristics equation of a matrix M be λ2 - λ - 1 =0, then
If  then find eigen values of the matrix I + A + A2, where I denotes the identity matrix
then find eigen values of the matrix I + A + A2, where I denotes the identity matrix
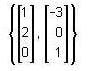
Let 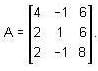 An eigenvalue of A is 2. Find a basis for the corresponding eigen space.
An eigenvalue of A is 2. Find a basis for the corresponding eigen space.
An arbitrary vector X is an eigen vector of the matrix
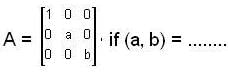
The values of λ and μ for which the equations x + y + z = 3, x + 3y + 2z = 6 and x + λy + 3z = μ have
If the matrix B is obtained from the matrix A by interchanging two rows, then-
Let V be the vector space of polynomials with degree not exceeding two. Let S = {1, x -1, x2 - 2x + 1} be a subset of V. Then which of the following(s) is/are true ?
Let  and
and 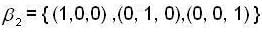 be ordered basis of
be ordered basis of 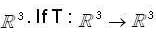 be a linear transformation such that
be a linear transformation such that 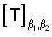
The matrix of T w.r. to basis β1 and β2 is  then which of the followings is /are correct ?
then which of the followings is /are correct ?
If matrix 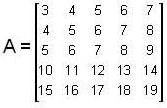 then the rank of the matrix A is _____________.
then the rank of the matrix A is _____________.
If A be an invertible matrix and Suppose that the inverse of 7 A is 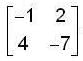 then the determinant of matrix A is ___________.
then the determinant of matrix A is ___________.
If 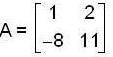 has the eigen values 3 and 9 then the sum o f the eigen values of A3 is __________.
has the eigen values 3 and 9 then the sum o f the eigen values of A3 is __________.
The number of distinct real roots of 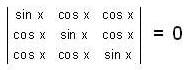 in the interval
in the interval 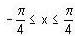 is __________.
is __________.
The sum of distinct characteristic roots of the matrix 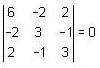 is _______.
is _______.
If 3, - 2 are the eigen values of a non-singular matrix A and |A| = 4, then the sum of the eigen values o f adj(A) are ________ .
The system of linear equations
(4d - 1) x + y + z = 0, - y + z = 0, (4d - 1 )z = 0 has a non-trivial solution, if the value of d is ___ .
Find the value of a for which the following system of equations over R is inconsistent.
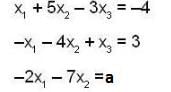
If V is a vector space over an infinite field F such that dim V = 2, then the number of distinct subspaces V has ________.
The dimension of the subspace of R3 spanned by (-3,0, 1), (1, 2, 1) and (3, 0, - 1 ) is ______ .


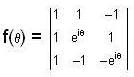 , then
, then 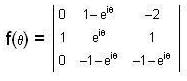
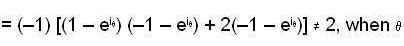
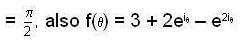
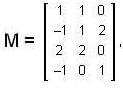 , then the rank of M is equal to
, then the rank of M is equal to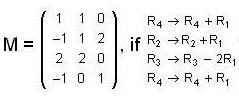
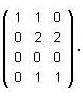
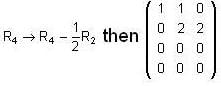
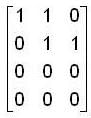

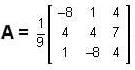 , then
, then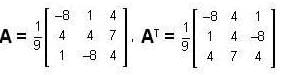
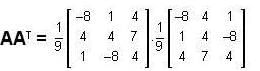
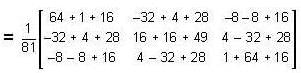
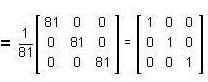
 , then the matrix A is equal to
, then the matrix A is equal to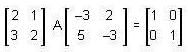
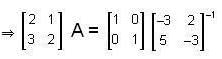
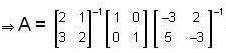
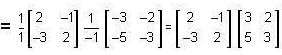
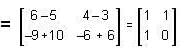
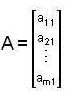 and B = [b11 b12 b13..... b1n] be two non-zero columns and row matrices respectively.
and B = [b11 b12 b13..... b1n] be two non-zero columns and row matrices respectively.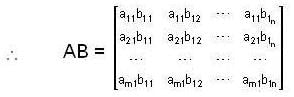
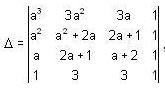 then
then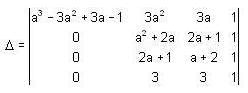
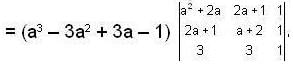

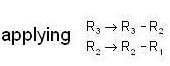
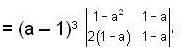 expanding with respect to the third column
expanding with respect to the third column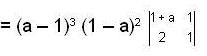

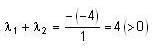

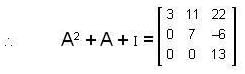
 Row reduce the augmented matrix for (A - 2i)x = 0.
Row reduce the augmented matrix for (A - 2i)x = 0.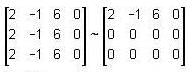
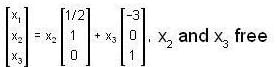
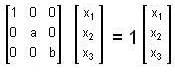
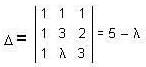
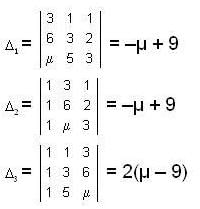
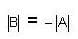
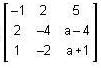 is
is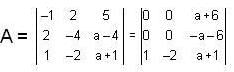
 When
When

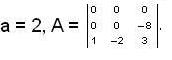
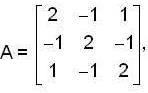 then
then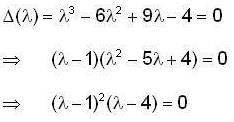
 co rresponding to λ = 1 .
co rresponding to λ = 1 . 
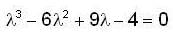
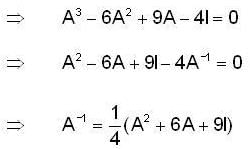
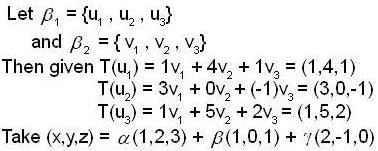
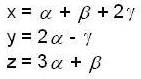
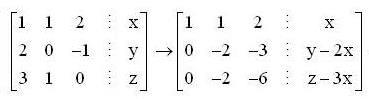

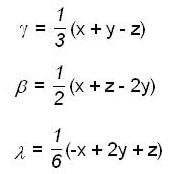
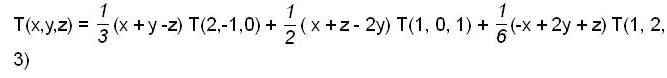
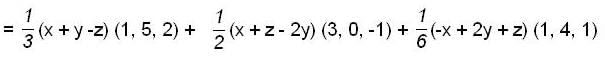
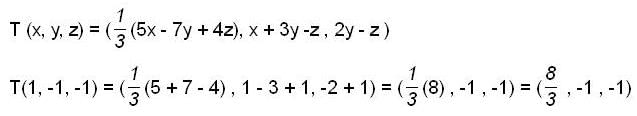
 we have
we have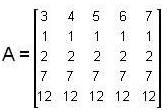
 wee have
wee have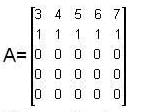
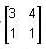 of order 2 whose value = 3 - 4 = -1 ≠0
of order 2 whose value = 3 - 4 = -1 ≠0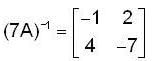
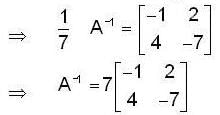
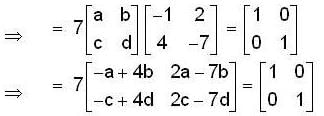
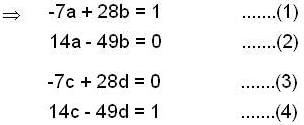
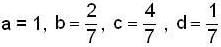
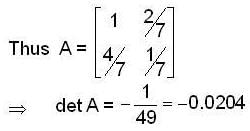
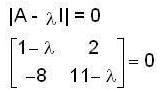
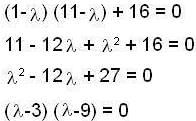
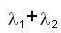 = 27+729 = 756
= 27+729 = 756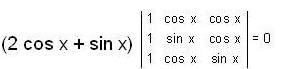 or
or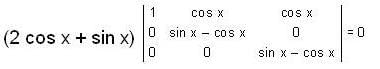

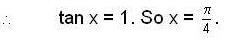


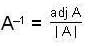 and if λ is eigen value of A, then λ-1 is eigen value of A-1.
and if λ is eigen value of A, then λ-1 is eigen value of A-1.