IIT Jam Mathematics Mock Test - 5 - Mathematics MCQ
30 Questions MCQ Test - IIT Jam Mathematics Mock Test - 5
The wronskian of two solutions of the differential equation t2y'' - t(t+2)y' + (t+2)y = 0 satisfies W (1) = 1 is
Let S be the surface of the paraboloid z =1- x2 - y2 with the domainof definition x2 +y2 ≤1 and be the boundary of the paraboloid. Given  then
then 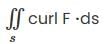
 then
then 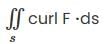
Which of the following must be true of a continuous function on (a, b)?
Let G be a non abelian group of order 21. Let 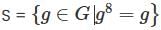 Then the number of non identity elements in S is
Then the number of non identity elements in S is
The number of proper normal subgroup of order 65 is
Consider the statements:
S1: Let G be an abelian group of order n if for every divisior m of n there exist a subgroup of G of order m, then G is cyclic.
S2,: Let G be a group. If every proper sub group of G is cyclic then G is abelian.
Which of the following is true.
The line integral of 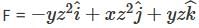 along the helix
along the helix 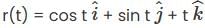 from t = 0 to t = 2π is
from t = 0 to t = 2π is
Which of the following is not correct for a positive term series:
The general solution of the equation y' = y (log y-1) is
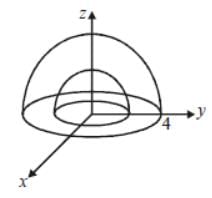
Evaluate 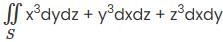 where S is the boundary of the volume V occupying the region between the spheres x2 + y2 + z2 =1 and x2 + y2 + z2 = 4 and above the plane z=0.
where S is the boundary of the volume V occupying the region between the spheres x2 + y2 + z2 =1 and x2 + y2 + z2 = 4 and above the plane z=0.
Let A be a 3 x 3 matrix whose columns are linearly dependent (i.e. columns lie in one plane). Then consider the two statements:
(I) Any vector which is a linear combination of the columns of A lies in the same plane.
(II) The system of equation Ax = b has at least one solution for any b ∈ ℝ3 Then
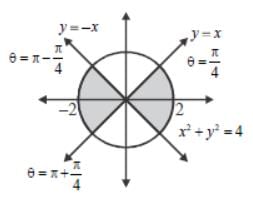
Let R be the region in ℝ2 determined by the inequalities x2 + y2 ≤ 4 and y2 ≤ x2, evaluate the following integral 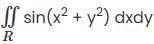
Let Pn (ℝ) be the vector space ofallpolynomials of degree atmost n.
Define T : P1 (ℝ)→ ℝ2 by T (p(x)) = (p(0)-2p(1), p(0) + p(0)). Then
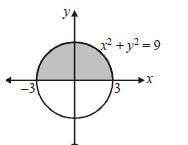
Determine the volume generated when the area above thex-axis bounded by the curve x2 + y2 = 9 and the co-ordinates x = 3 and x = -3 is rotated aboutx axis.
The number of subgroups oforderp in ℤp × ℤp × ℤp is
Length of the curve y = x3/2 from point (0,0) to (4, 8) is equal to
Let Pn (ℝ) be the vector space of all polynomials of degree atmost n.
Let g(x) = x + 1 and define T : P2 (ℝ)→P2 (ℝ) by
T(f (x)) = f'(x) g(x) + 2f (x).
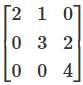
Then the trace of A is;
he number of real root of the equation x5 + x3 - 2 = 0 is
Let f :ℝ→ℝ be a continuous map, choose the correct statement
Which of the following functions is not uniformly continuous?
Consider w = f(z) = u(x, y) + i v(x, y) to be an analytic function in a domain D. Which one of the following options is NOT correct?
Cosider the initial value problem y" +2y' +6y = 0, y(0) =2; y' (0) = α ≥ 0. Let x(��) be the smallest possible value of x, for which y= 0. Then 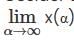 is
is


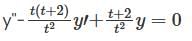
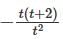
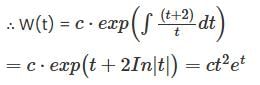
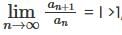 then
then 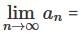
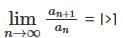
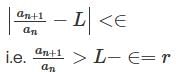
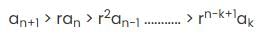
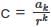 then we have
then we have 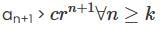
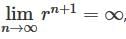 , and hence
, and hence 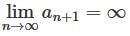

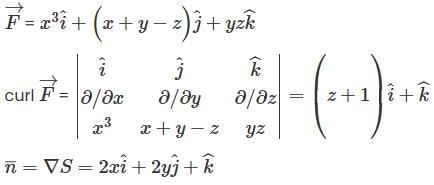
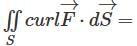
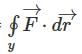
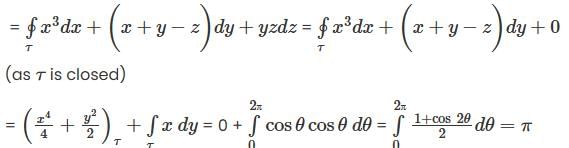
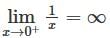 or, hence both (a) and (b) are incorrect
or, hence both (a) and (b) are incorrect
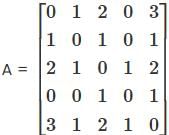 then
then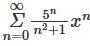 is
is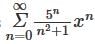
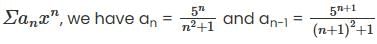
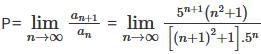
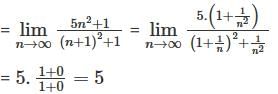
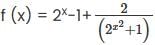
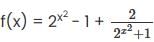
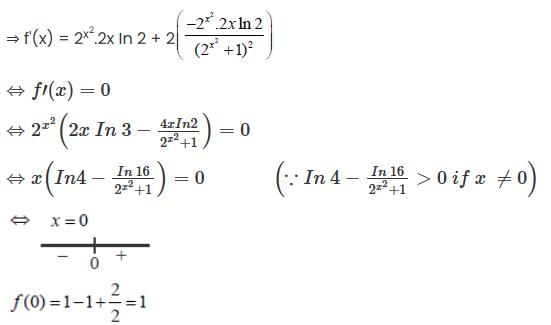
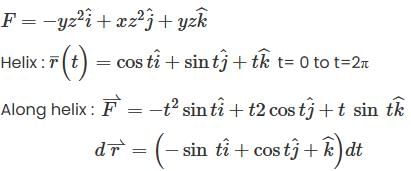


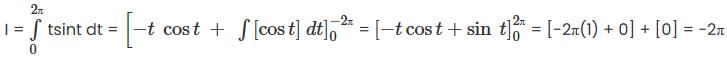
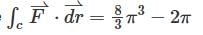
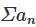 .
.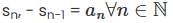
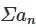 converges, hence its sequence of partial sum is convergent.
converges, hence its sequence of partial sum is convergent.
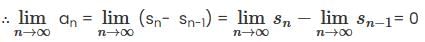
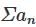 , and
, and 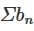 respectively. Then
respectively. Then be the sequence of partial sum of
be the sequence of partial sum of 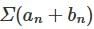 .
.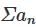 , converges, hence (sn) is convergent. Also
, converges, hence (sn) is convergent. Also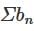 diverges, so (tn) is divergent.
diverges, so (tn) is divergent.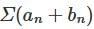 diverges.
diverges.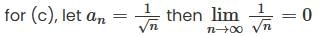
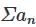 diverges.
diverges.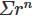 converges only when |r|<1.
converges only when |r|<1.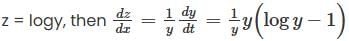
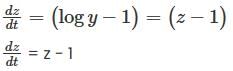
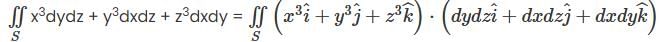 (by definition this is resolution of
(by definition this is resolution of  into rectangular components.)
into rectangular components.)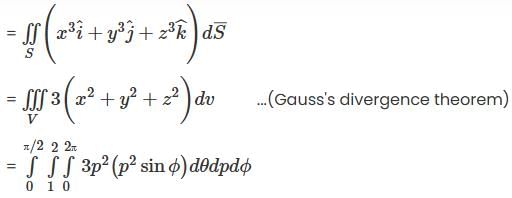

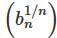 where
where 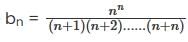 converges to
converges to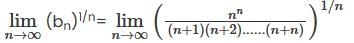
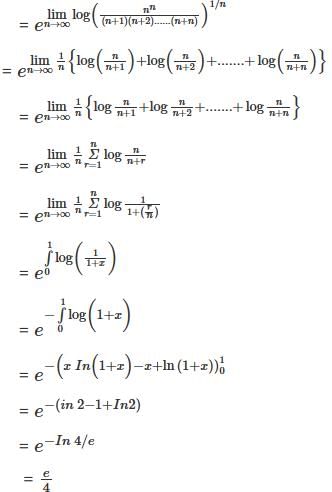
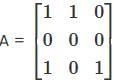
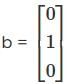
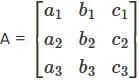
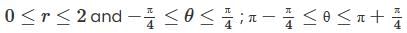
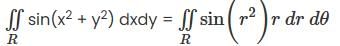
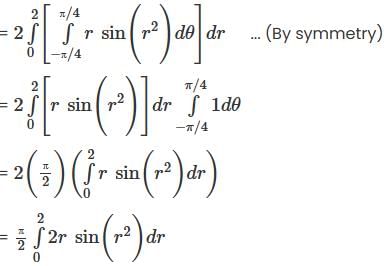
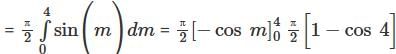
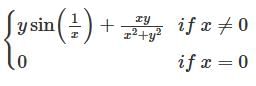
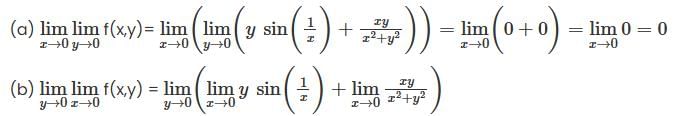
 do not exist
do not exist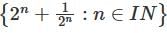 is
is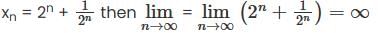
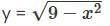
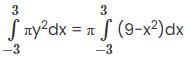
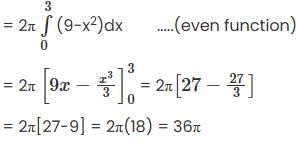
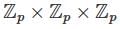 is p3 -1
is p3 -1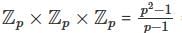 = p2 + p + 1.
= p2 + p + 1.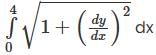
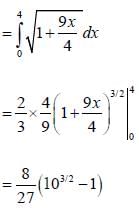
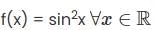
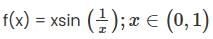
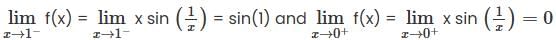
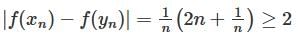
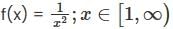
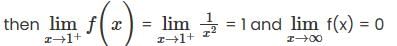
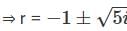
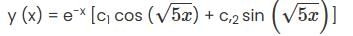
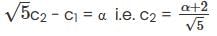
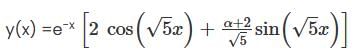
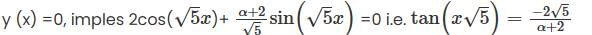
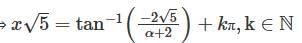
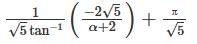
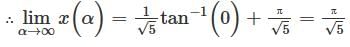
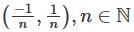
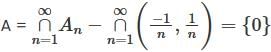 is not open.
is not open.










