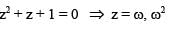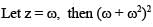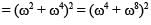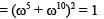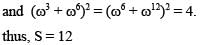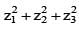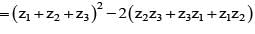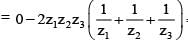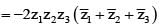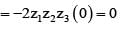JEE Advanced Level Test: Complex Number- 2 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Complex Number- 2
If (a + bi)11 = x + iy, where a, b, x, y ∈ R , then (b + ai)11 equals
If (a1 +ib1)(a2 +ib2) ....(an + ibn) = A +iB, then  is equal to
is equal to
If ω is a complex cube root of unity, then the value of  is
is
The complex numbers sin x + i cos 2x and cos x – i sin 2x are conjugate to each to other, for
If z = 1 + i tan a , where 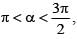 then |z| is equal to
then |z| is equal to
If in polar form z1 = cos α + i sin α, z2 = cos β + i sin β, z3 = cos γ + i sin γ and z1 + z2 + z3 = 0 , then 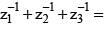
If |z1 - 1| < 1, |z2 - 2|, 2, |z3 - 3|< 3, then |z1 + z2 +z3|
If a is the nth root of unity, then 1 + 2a + 3a2 + ...... to n terms equal to
If 1, ω, ω2, ...ωn -1are nth roots of unity, then (1 - ω)(1 - ω2)...(1 - ωn-1) is equal to
W is cube root of unity (ω ≠ 1) then the value of ωn + ωn+1 + ωn+2 is (n ∈ N)
If α and β are different complex numbers with , then
is equal to
For any two non-zero complex numbers z1 and z2 if then the difference of amplitudes of z1 and z2 is
Let z be a purely imaginary number such that Im(z) < 0. Then arg(z) is equal to
For any complex number z, maximum value of |z| – |z – 1| is
If a, b are the roots of x2 + px + q = 0, and w is a cube root of unity, then value of (ωα + ω2β)(ω2α + ωβ) is
If ω (≠1) is a cube root of unity and (1 + ω2)11 = a + bω + cω2, then (a, b, c) equals
If (ω ≠1) is a complex cube root of unity and (1 + ω4)n = (1 + ω8)n , then the least possible integral value of n is
If α (≠ 1) is a fifth root of unity and b (≠ 1) is a fourth root of unity, then z = (1 + α) (1 + β) (1 + α2) (1 + β2) (1 + α3) (1 + β3) equals
The number of complex numbers satisfying 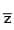 = iz2 is
= iz2 is
If z2 + z + 1 = 0, where z is a complex number, then value of
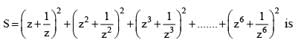
If z1 + z2 + z3 = 0 and |z1| = |z2| = |z3| = 1, then value of equals


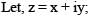
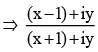
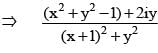
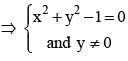
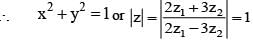
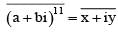
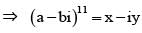
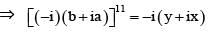

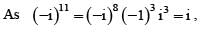 we get
we get 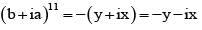

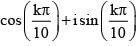 , then z1z2z3z4 is equal to
, then z1z2z3z4 is equal to 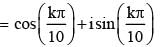
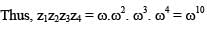
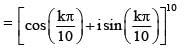
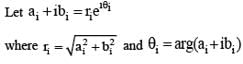
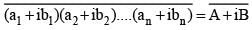
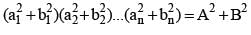
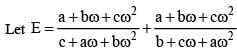

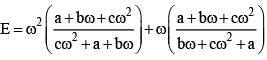
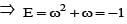
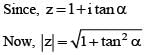
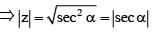
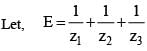
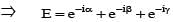
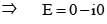 [(Using (i)]
[(Using (i)]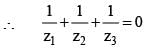
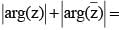
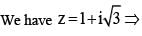
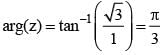
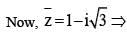
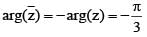
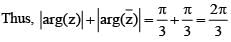
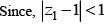
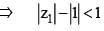 (Triangle Inequality)
(Triangle Inequality)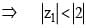 ....(i)
....(i)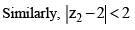
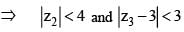 ....(ii)
....(ii)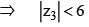

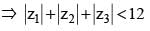
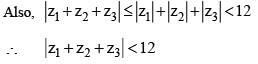
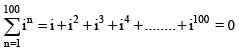
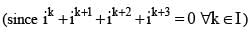
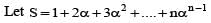
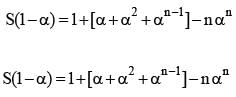
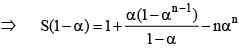
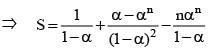
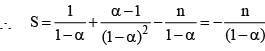
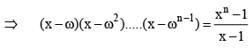
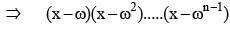
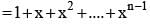
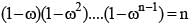
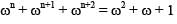

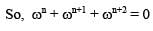
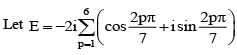
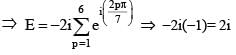
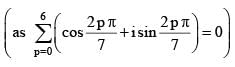
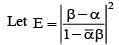
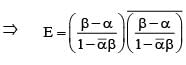
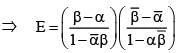
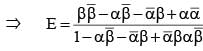

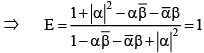
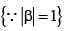
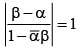
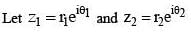
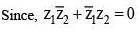
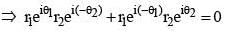
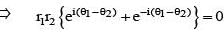
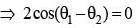
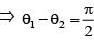
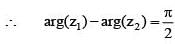
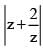 is
is 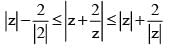
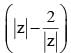 i is an increasing function of |z| and |z| > 5
i is an increasing function of |z| and |z| > 5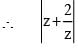 will take its minimum value at z = 5
will take its minimum value at z = 5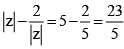
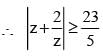
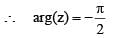
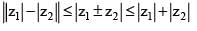 (given)
(given)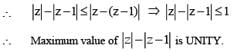
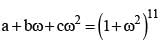
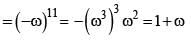
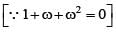
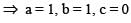
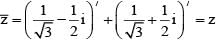
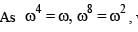
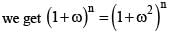
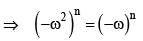
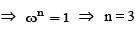
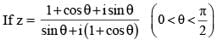 then |z| equals
then |z| equals
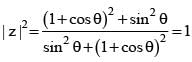
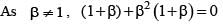
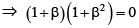
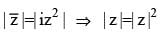
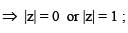

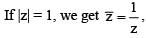
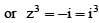
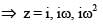 where ω (≠1) is a cube root of unity.
where ω (≠1) is a cube root of unity.