JEE Advanced Level Test: Continuity and Differentiability- 1 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Continuity and Differentiability- 1
A function f(x) is defined as below
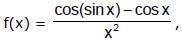 x ≠ 0 and f(0) = a, f(x) is continuous at x = 0 if a equals
x ≠ 0 and f(0) = a, f(x) is continuous at x = 0 if a equals
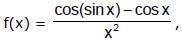 x ≠ 0 and f(0) = a, f(x) is continuous at x = 0 if a equals
x ≠ 0 and f(0) = a, f(x) is continuous at x = 0 if a equals 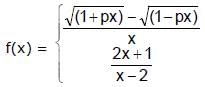 , -1 ≤ x < 0 is continuous in the interval [–1, 1], then `p' is equal to:
, -1 ≤ x < 0 is continuous in the interval [–1, 1], then `p' is equal to:
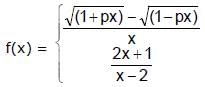 , -1 ≤ x < 0 is continuous in the interval [–1, 1], then `p' is equal to:
, -1 ≤ x < 0 is continuous in the interval [–1, 1], then `p' is equal to:Let f(x) = 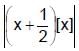 when – 2 ≤ x ≤ 2. Then (where [ * ] represents greatest integer function)
when – 2 ≤ x ≤ 2. Then (where [ * ] represents greatest integer function)
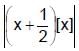 when – 2 ≤ x ≤ 2. Then (where [ * ] represents greatest integer function)
when – 2 ≤ x ≤ 2. Then (where [ * ] represents greatest integer function)Let f(x) = sgn (x) and g(x) = x (x2 – 5x + 6). The function f(g(x)) is discontinuous at
If y = 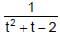 where t =
where t =  , then the number of points of discontinuities of y = f(x), x ∈ R is
, then the number of points of discontinuities of y = f(x), x ∈ R is
The equation 2 tan x + 5x – 2 = 0 has
If f(x) = 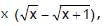 , then indicate the correct alternative(s)
, then indicate the correct alternative(s)
The function f (x) = 1 + | sin x l is
If f(x) = 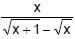 be a real valued function then
be a real valued function then
The function f(x) = sin-1 (cos x) is
Let f(x) be defined in [–2, 2] by f(x) = 
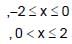 then f(x)
then f(x)
If f(x) is differentiable everywhere, then
Let f(x + y) = f(x) f(y) all x and y. Suppose that f(3) = 3 and f'(0) = 11 then f'(3) is given by
If f : R → R be a differentiable function, such that f(x + 2y) = f(x) + f(2y) + 4xy 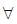 x, y ∈ R, then
x, y ∈ R, then
Let f(x) = x – x2 and g(x) = 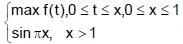 . Then in the interval [0, ¥)
. Then in the interval [0, ¥)
Let [x] denote the integral part of x ∈ R and g(x) = x – [x]. Let f(x) be any continuous function with f(0) = f(1) then the function h(x) = f(g(x))
If f (x) = [x sin p x] { where [x] denotes greatest integer function}, then f (x) is
If f(x) =  , then f(x) is
, then f(x) is
The functions defined by f(x) = max {x2, (x – 1)2, 2x (1 – x)}, 0 £ x £ 1
Let f(x) = x3 – x2 + x + 1 and g(x) =  then
then
Let f²(x) be continuous at x = 0 and f²(0) = 4 then value of  is
is
Let f : R → R be a function such that f , f(0) = 0 and f¢(0) = 3, then
Suppose that f is a differentiable function with the property that f(x + y) = f(x) + f(y) + xy and  f(h) = 3 then
f(h) = 3 then
If a differentiable function f satisfies f
x, y Î R, find f(x)
Let f : R → R be a function defined by f(x) = Min {x + 1, |x| + 1}. Then which of the following is true ?
The function f : R /{0} → R given by vf(x) = 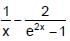 can be made continuous at x = 0 by defining f(0) as
can be made continuous at x = 0 by defining f(0) as
Function f(x) = (|x – 1| + |x – 2| + cos x) where x Î [0, 4] is not continuous at number of points
Let f(x + y) = f(x) f(y) for all x, y, where f(0) ≠ 0. If f'(0) = 2, then f(x) is equal to
A function f : R → R satisfies the equation f(x + y) = f(x) . f(y) for all x, y ∈ R, f(x) ≠ 0. Suppose that the function is differentiable at x = 0 and f'(0) = 2 then f'(x) =
Let f(x) = [cos x + sin x], 0 < x < 2p where [x] denotes the greatest integer less than or equal to x. the number of points of discontinuity of f(x) is





















