JEE Advanced Level Test: Matrices & Determinants - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Matrices & Determinants
The number of different orders of a matrix having 12 elements is
If A and B are square matrices of order 2, then (A + B)2 equal to
If A is a skew – symmetric matrix, then trace of A is equal to
Which of the following is a vector?
If A is a square matrix such that A2 = then A–1 equal to
If A and B are square matrices of order 3 such that |A| = –1, |B| = 3, then |3AB| is equal to
If 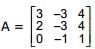 , then value of A-1 is equal to
, then value of A-1 is equal to
If the order of matrix A is m×p. And the order of B is p×n. Then the order of matrix AB is?
The system of equation –2x + y + z = 1, x – 2y + z = –2, x + y + λz = 4 will have no solution if
The system of the linear equations x + y – z = 6, x + 2y – 3z = 14 and 2x + 5y – λz = 9 (λ ∈ R) has a unique solution if
If A = diag (2, –1, 3), B = diag (–1, 3, 2), then A2 B equal to
If the matrix AB is a zero matrix, then
If AB = A and BA = B, then B2 is equal to
If A and B are symmetric matrices, then ABA is
If A is a skew – symmetric matrix and n is an even positive integer, then An is
If A is a non–singular matrix and AT denotes the transpose of A, then
Which of the following is incorrect
If A is square matrix of order 3, then the true statement is (where l is unit matrix).
The transpose of a column matrix is a :
From the matrix equation AB = AC, we conclude B = C provided
Which of the following property of matrix multiplication is correct:
If 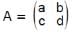 satisfies the equation x2 – (a + d) x + k = 0, then
satisfies the equation x2 – (a + d) x + k = 0, then
Which of the following is a nilpotent matrix



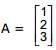 and
and 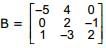 , then
, then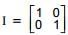 ,
, 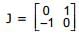 and
and 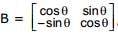 , then B equal to
, then B equal to 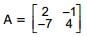 and
and 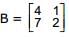 then BTAT is
then BTAT is










