JEE Advanced Level Test: Trigonometric Equations- 2 - Airforce X Y / Indian Navy SSR MCQ
25 Questions MCQ Test - JEE Advanced Level Test: Trigonometric Equations- 2
If 20 sin2θ + 21 cos θ – 24 = 0 & 7π/4 < θ < 2π then the values of cot θ/2 is
The general solution of the equation tan x + tan 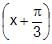 + tan
+ tan 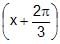 = 3 is
= 3 is
The general solution of the equation tan2 a + 2 √3 tan a = 1 is given by
Total number of solutions of sin x . tan 4x = cos x belonging to (0, π) are
If 2 tan2x – 5 sec x – 1 = 0 has 7 different roots in , n ∈ N, then greatest value of n is
The values of x between 0 and 2p which satisfy the equation sinx . = 1 are in A.P. The common difference of the A.P. is
Equation of the form P (sinx ± cosx, sinx cosx) = 0 where P(y, z) is a polynomial, can be solved by the change :
cos x ± sin x = t ; 1 ± 2 sin x cos x = t2. Reduce the given equation into P = 0
sin x + cos = 1 + sin x cos x is
If (cos x – sin x) + 2 = 0, then x is
sin4x + cos4x = sin x cos x then x is–
The minimum value of 27cos2x 81sin2x is
Number of roots of the equation cos7 x + sin4 x = 1 in the interval [0, 2π] is
The smallest positive number of π for whcih the equation cos (π sin x) = sin (π cos x) has a solutionin [0, 2π] is
If sin θ + 7 cos θ = 5, then tan (θ/2) is a root of the equation
Match the following for number of solutions in [0, 2p]
Column - I Column - II
(A) sin2 q _ tan2 q = 1 (P) 2
(B) sin q + cos q = 1 (Q) 0
(C) tan q + sec q = 2cosq (R) 3
(D) 3sin2q _ 4 sinq + 1 = 0 (S) 1
What are the most general values of q which satisfy the equations,
(a) sin q = (b) tan (x _ 1) =
(c) tanq = _1 (d) cosec q =
(e) 2cot2q = cosec2q
If 0 < t < 2π and sin t = - 1, then t =
Solve : cot q + tan q = 2 cosec q
Solve : tan2q _ (1 + ) tan q +
= 0
Find all the angles between 0º and 90º which satisfy the equation sec2q . cosec2q + 2 cosec2q = 8
Solve : 4 cos q _ 3 sec q = 2 tan q
Solve : sin q + sin 3q + sin 5q = 0














