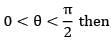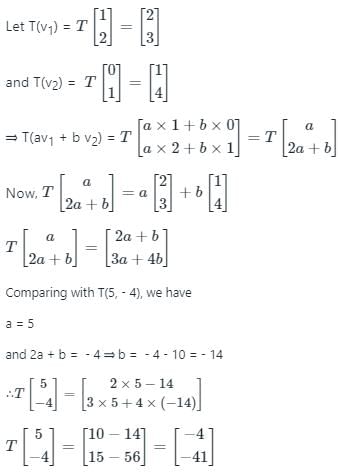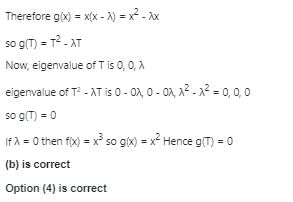Linear Transform MCQ - 2 - IIT JAM MCQ
30 Questions MCQ Test - Linear Transform MCQ - 2
Let V be vector space of real polynomials of degree atmost 2. Define a linear operator 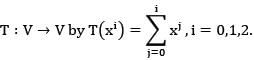 The matrix of T-1 with respect to the basis {1, x, x2} is
The matrix of T-1 with respect to the basis {1, x, x2} is
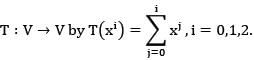 The matrix of T-1 with respect to the basis {1, x, x2} is
The matrix of T-1 with respect to the basis {1, x, x2} isFor a positive integer n let 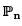 denotes the vector space of polynomials in one variable x with real coefficients and with degree less than n. Consider the map
denotes the vector space of polynomials in one variable x with real coefficients and with degree less than n. Consider the map 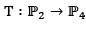 defined byT(p(x)) = p(x2).Then
defined byT(p(x)) = p(x2).Then
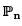 denotes the vector space of polynomials in one variable x with real coefficients and with degree less than n. Consider the map
denotes the vector space of polynomials in one variable x with real coefficients and with degree less than n. Consider the map 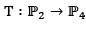 defined byT(p(x)) = p(x2).Then
defined byT(p(x)) = p(x2).ThenLet V be the space of twice differentiable functions of  satisfying f" - 2f' + f = 0. Define
satisfying f" - 2f' + f = 0. Define  by T(f) = (f'(0), f(0)).Then T is
by T(f) = (f'(0), f(0)).Then T is
 satisfying f" - 2f' + f = 0. Define
satisfying f" - 2f' + f = 0. Define  by T(f) = (f'(0), f(0)).Then T is
by T(f) = (f'(0), f(0)).Then T isLet T be a 4 x 4 real matrix such that T4 = 0. Let ki = dim(kerTi) for 1 < i < 4 which of the following is not a possibility for the sequence k1 < k2 < k3 < k4?
Let  be a linear transformation. Which of the following statement implies that T is bijective?
be a linear transformation. Which of the following statement implies that T is bijective?
Let 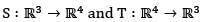 be linear transformation such that T ° S is the identity map of
be linear transformation such that T ° S is the identity map of 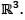 Then
Then
Let n be a positive integer and let 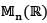 denotes the space of all n x n real matrices. If
denotes the space of all n x n real matrices. If 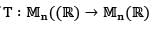 is a linear transformation such thatT(A) = 0 whenever
is a linear transformation such thatT(A) = 0 whenever 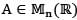 is symmetric or skew symmetric then the rank of T is
is symmetric or skew symmetric then the rank of T is
Let A be a 3 × 3 matrix with eigenvalues 1, –1 and 3. Then
Let S = {T: R3 → R3; T is a linear transformation with T (1, 0, 1) = (1, 2, 3) and T (1, 2, 3) = (1, 0, 1). Then S is
Let 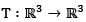 be the linear transformation defined by T(x1, x2, x3) = (x1 + 3x2 + 2x3, 4x2 + x3, 2x + x2 - x3). The dimension of null space of T3 is
be the linear transformation defined by T(x1, x2, x3) = (x1 + 3x2 + 2x3, 4x2 + x3, 2x + x2 - x3). The dimension of null space of T3 is
Let the linear transformation 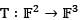 be defined by T(x1, x2) = (x1, x2 + x2, x2). Then the nullity of T is
be defined by T(x1, x2) = (x1, x2 + x2, x2). Then the nullity of T is
Let T be an arbitrary linear transformation from 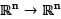 which is not one one then
which is not one one then
Let 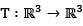 be the linear transformation defined by T(x1, x2, x3) = (x1+ 3x2 + 2x3, 3x1 + 4x2 + x3, 2x1 + x2 - x3).The dim ension of the null space of T2 is
be the linear transformation defined by T(x1, x2, x3) = (x1+ 3x2 + 2x3, 3x1 + 4x2 + x3, 2x1 + x2 - x3).The dim ension of the null space of T2 is
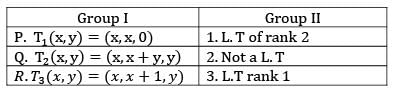
Choose the correct matching from a, b. c and d for the transformation T1, T2 and T3 as defined in group I with the statements given in group II
Let T (x, y, z) = xy2 + 2z – x2z2 be the temperature at the point (x, y, z). The unit vector in the direction in which the temperature decrease most rapidly at (1, 0, – 1) is
Let T: R4 → R4 be a linear transformation satisfy T3 + 3T2 = 4I, where I is the identity
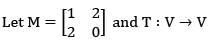 be the linear map defined by T (A) = AM where V be the vector space of all 2 x 2 real matrices. Then rank and nullity of T respectively
be the linear map defined by T (A) = AM where V be the vector space of all 2 x 2 real matrices. Then rank and nullity of T respectively
Let T be a linear transformation from a vector space 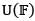 into a vector space
into a vector space 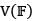 with U as finite dimensional. The rank of T is the dimension of the
with U as finite dimensional. The rank of T is the dimension of the
Let a matrix Amxn represents a linear mapping T : Vn → Vm.Then range ofT is generated by
Let T : R2 → R2 be a linear transformation such that T((1, 2)) = (2, 3) and T((0, 1)) = (1, 4).Then T((5, -4)) is
Let T be a linear operator on ℝ3. Let f(X) ∈ ℝ[X] denote its characteristic polynomial. Consider the following statements.
(a). Suppose T is non-zero and 0 is an eigen value of T. If we write f(X) = X g(X) in ℝ[X], then the linear operator g(T) is zero.
(b). Suppose 0 is an eigenvalue of T with at least two linearly independent eigen vectors. If we write f(X) = X g(X) in ℝ[X], then the linear operator g(T) is zero.
The matrix A is represented asThe transpose of the matrix of this matrix is represented as?
Let 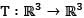 be a linear transformation given by T(x, y, z) = (x, y, 0). Then the null space is generated by which one of the following?
be a linear transformation given by T(x, y, z) = (x, y, 0). Then the null space is generated by which one of the following?
Let 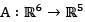 and
and 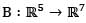 be two linear transformation. Then which of the following can be true?
be two linear transformation. Then which of the following can be true?
What is the rank of the linear transformation 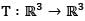 defined by T(x, y, z) = (y, 0, z)?
defined by T(x, y, z) = (y, 0, z)?
Consider the linear map 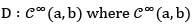 is the set of all real valued continuously differential functions defined by D(f) = f' then
is the set of all real valued continuously differential functions defined by D(f) = f' then
Consider the linear transformation  is given by T(x, y, z, u) = (x, y, 0, 0). Then which one of the following is correct?
is given by T(x, y, z, u) = (x, y, 0, 0). Then which one of the following is correct?
Let the linear transform ations S and 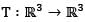 be defined by
be defined by
S(x, y, z) = (2x, 4x - y, 2x + 3y - z)
T(x, y, z) = (x cosθ - y sinθ, sinθ + y cos θ, z) where