Linear Transform MCQ - 5 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Linear Transform MCQ - 5
If the characteristic polynomial of A is given by Δ(λ) = λ3 - λ2 + 2λ+ 28. Then trace of A and determinant of A are respectively
The eigenvalues of a 3 x 3 real matrix A are 1, 2 and - 3. Then
Let A be a matrix with complex enteries. If A is hermitian as well as unitary and α is an eigen values of A then
Let P and Q be square matrices such that PQ = I the identity matrix, then zero is an eigenvalue of
Let M be a skew symmetric orthogonal real Matrix. Then only possible eigenvalues are
Let A be a 3 x 3 real matrix such that A2 = -I3 where I3 is the 3 x 3 identity matrix then a matrix A is
If A and B are symmetric matrices of the same order, then (AB′ – BA′) is a
If M is a 3 x 3 real matrix that satisfies M3 = M then
(I) M is invertible
(II) Eigenvalues of M are distinct
(III) M is singular
Select the correct code
For a 3 x 3 real matrix. Let C(A) denotes the set of the real characteristic roots of A. Suppose C(B) = C(B-1) fora non singular matrix B with no repeated eigenvalues then
The eigenvalues of a 3 x 3 real matrix P are 1, - 2, 3, then
If A and B are square matrices of different order Cx(A) and cx(B) are characteristic polynomials of A and B respectively and it is given that Cx(B) is minimal polynomial of A as well then
Let U be a 3 X 3 complex Hermitian matrix which is unitary. Then the distinct eigenvalues of U are
|
27 docs|150 tests
|


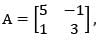 , which of ihe following is not correct?
, which of ihe following is not correct?