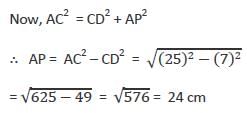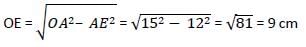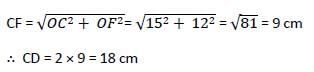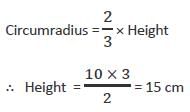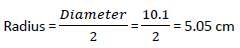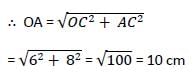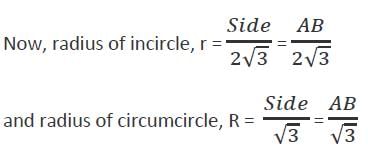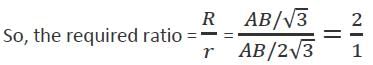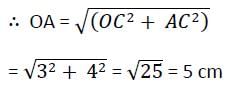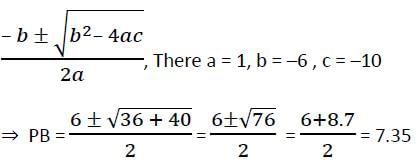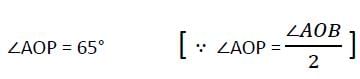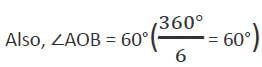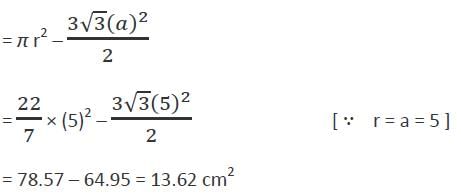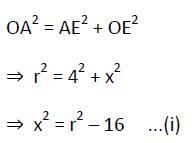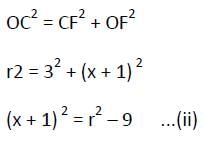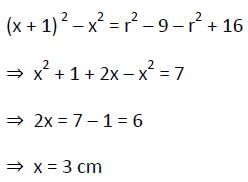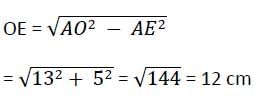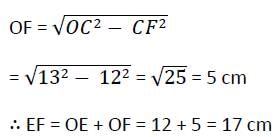Explore Exams
Login Signup
Sign in Open App
RRB NTPC/ASM/CA/TA Exam  >  RRB NTPC/ASM/CA/TA Tests  >  Mathematics for RRB NTPC (Hindi)  >  MCQ: वृत्त - 1 - RRB NTPC/ASM/CA/TA MCQ

MCQ: वृत्त - 1 - RRB NTPC/ASM/CA/TA MCQ


Test Description

15 Questions MCQ Test Mathematics for RRB NTPC (Hindi) - MCQ: वृत्त - 1

MCQ: वृत्त - 1 for RRB NTPC/ASM/CA/TA 2025 is part of Mathematics for RRB NTPC (Hindi) preparation. The MCQ: वृत्त - 1 questions and answers have been prepared according to the RRB NTPC/ASM/CA/TA exam syllabus.The MCQ: वृत्त - 1 MCQs are made for RRB NTPC/ASM/CA/TA 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for MCQ: वृत्त - 1 below.
Solutions of MCQ: वृत्त - 1 questions in English are available as part of our Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA & MCQ: वृत्त - 1 solutions in Hindi for Mathematics for RRB NTPC (Hindi) course. Download more important topics, notes, lectures and mock test series for RRB NTPC/ASM/CA/TA Exam by signing up for free. Attempt MCQ: वृत्त - 1 | 15 questions in 15 minutes | Mock test for RRB NTPC/ASM/CA/TA preparation | Free important questions MCQ to study Mathematics for RRB NTPC (Hindi) for RRB NTPC/ASM/CA/TA Exam | Download free PDF with solutions
MCQ: वृत्त - 1 - Question 1
Save

निर्देश: कृपया निम्नलिखित प्रश्नों का ध्यानपूर्वक अध्ययन करें और सही उत्तर चुनें:

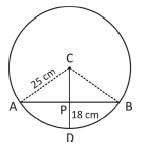
सी का केंद्र होने वाले वृत्त का व्यास 50 सेमी है। CP वृत्त का एक कर्ण खंड है। AB एक श्रेणी है जो CP के प्रति लंब और P से गुजरती है। CP का विस्तार D पर वृत्त को काटता है। यदि DP = 18 सेमी है, तो AB की लंबाई क्या है?

Detailed Solution for MCQ: वृत्त - 1 - Question 1

त्रिकोण ACP में
CP = CD - PD = 25 - 18 = 7

इसी प्रकार, PB = 24 सेमी
इसलिए, AB = AP + PB
= 24 + 24
= 48 सेमी।
इसलिए, विकल्प D सही है।

MCQ: वृत्त - 1 - Question 2
Save

निर्देश: कृपया निम्नलिखित प्रश्नों का सावधानीपूर्वक अध्ययन करें और सही उत्तर चुनें:

दो समान वृत्त जिनकी त्रिज्या 4 सेमी है, एक-दूसरे को इस तरह काटते हैं कि प्रत्येक दूसरे के केंद्र से होकर गुजरता है। सामान्य तलों की लंबाई है:

Detailed Solution for MCQ: वृत्त - 1 - Question 2

प्रश्न के अनुसार, हम 4 सेमी त्रिज्या के दो समान वृत्तों का चित्र बनाते हैं जो एक-दूसरे को इस तरह काटते हैं कि प्रत्येक दूसरे के केंद्र से होकर गुजरता है,

OC = 2 सेमी
OA = 4 सेमी
इसलिए, AC = √(OA² - OC²)
इसलिए, AC = √(4² - 2²) = √(16 - 4)
AC = √12 = 2√3
इसलिए, AB = 4√3 सेमी

Clear all your doubts with EduRev
MCQ: वृत्त - 1 - Question 3
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

एक वृत्त में 30 सेमी व्यास वाली दो समानांतर तंतु खींचे गए हैं। एक तंतु की लंबाई 24 सेमी है और दोनों तंतुओं के बीच की दूरी 21 सेमी है। दूसरे तंतु की लंबाई क्या है?

Detailed Solution for MCQ: वृत्त - 1 - Question 3

दिया गया है, एक तंतु AB = 24 सेमी
तो, AE = EB = 12 सेमी
व्यास = 30 सेमी ⇒ त्रिज्या, AO = OC = 15 सेमी
ΔAOE से, पायथागोरस प्रमेय के अनुसार

दो तंतुओं के बीच की दूरी, EF = 21 सेमी (दिया गया)
अतः OF = EF – OE = 21 – 9 = 12 सेमी
ΔCOF से, पायथागोरस प्रमेय के अनुसार

इसलिए, विकल्प B सही है।

MCQ: वृत्त - 1 - Question 4
Save

निर्देश: कृपया निम्नलिखित प्रश्न का ध्यानपूर्वक अध्ययन करें और सही उत्तर चुनें:

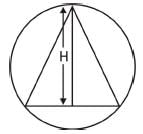
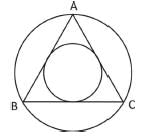
10 सेमी व्यास वाला एक वृत्त है जिसमें एक सम्बाहु त्रिकोण inscrit किया गया है। त्रिकोण के किसी भी पक्ष पर केंद्र से खींची गई लंबवत रेखा की लंबाई क्या होगी?
Detailed Solution for MCQ: वृत्त - 1 - Question 4

इसलिए,
केंद्र से खींची गई लंबवत रेखा की लंबाई
= 15 - 10 = 5 सेमी।
इसलिए, विकल्प D सही है।

MCQ: वृत्त - 1 - Question 5
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

एक वृत्त का सबसे बड़ा तंतु 10.1 सेंटीमीटर है। इस वृत्त का त्रिज्या होना चाहिए:
Detailed Solution for MCQ: वृत्त - 1 - Question 5

वृत्त का सबसे बड़ा तंतु उसका व्यास होता है। इसलिए,

इसलिए, विकल्प B सही है।

MCQ: वृत्त - 1 - Question 6
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

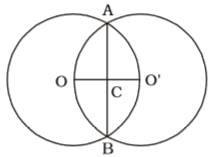
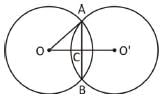
यदि दो समान वृत्त जिनके केंद्र O और O' हैं, एक दूसरे के साथ बिंदु A और B पर मिलते हैं, OO' = 12 सेमी और AB = 16 सेमी है, तो वृत्त की त्रिज्या क्या होगी?
Detailed Solution for MCQ: वृत्त - 1 - Question 6

दी गई जानकारी के अनुसार, AB = 16 सेमी और OO' = 12 सेमी
∴ AC = CB = 8 सेमी और OC = CO' = 6 सेमी
ΔAOC से, पायथागोरस के प्रमेय के अनुसार

इसलिए, विकल्प A सही है।

MCQ: वृत्त - 1 - Question 7
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

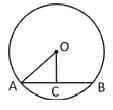
एक ΔABC में, AB = BC = CA। परिकल्पित वृत्त की त्रिज्या और अंतः वृत्त की त्रिज्या का अनुपात क्या है?
Detailed Solution for MCQ: वृत्त - 1 - Question 7

एक ΔABC में,
AB = BC = AC
इसलिए, ΔABC एक समभुज त्रिकोण है।
मान लीजिए कि r अंतः वृत्त की त्रिज्या है और R परिकल्पित वृत्त की त्रिज्या है।

= 2 : 1.
इसलिए, विकल्प A सही है।

MCQ: वृत्त - 1 - Question 8
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

एक वृत्त की तिर्यक की लंबाई 8 सेमी है और तिर्यक और केंद्र के बीच का लंबवत दूरी 3 सेमी है। फिर वृत्त की त्रिज्या कितनी है:
Detailed Solution for MCQ: वृत्त - 1 - Question 8

तिर्यक, AB = 8 सेमी
तब, AC = CB = 4 सेमी
केंद्र और तिर्यक के बीच का लंबवत दूरी,
OC = 3 सेमी

इसलिए, विकल्प B सही है।

MCQ: वृत्त - 1 - Question 9
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

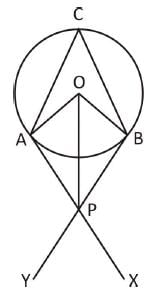
गोलाकार चक्र की तंतु AB और CD बाहरी रूप से P पर मिलते हैं। यदि AB = 6 सेमी, CD = 3 सेमी और PD = 5 सेमी है, तो PB की लंबाई क्या होगी?
Detailed Solution for MCQ: वृत्त - 1 - Question 9

दी गई जानकारी के अनुसार, PD = 5 सेमी है। फिर, PC = PD - CD = 5 - 3 = 2 सेमी।
इसी प्रकार, PA = (PB - 6) सेमी।
ध्यान दें: यदि दो तंतु AB और CD एक चक्र के भीतर या बाहर एक बिंदु P पर मिलते हैं, तो
PA x PB = PC x PD ⇒ (PB - 6) x PB = 2 x 5 ⇒ PB² - 6PB - 10 = 0।
श्रीधराचार्य सूत्र के द्वारा,

इसलिए, विकल्प B सही है।

MCQ: वृत्त - 1 - Question 10
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

निम्नलिखित कथनों पर विचार करें:
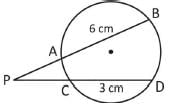
I. एक वृत्त की टेढ़ी एक रेखा है जो वृत्त को केवल एक ही बिंदु पर मिलती है।
II. व्यास के अंत बिंदु पर वृत्त की टेढ़ी व्यास के प्रति लंबवत होती है।
उपरोक्त में से कौन सा कथन सही है?
Detailed Solution for MCQ: वृत्त - 1 - Question 10

टेढ़ी की परिभाषा के अनुसार,
एक वृत्त की टेढ़ी एक सीधी रेखा है जो वृत्त को एक ही बिंदु पर छूती है। इसके अलावा, एक वृत्त के व्यास के अंत बिंदुओं पर टेढ़ी व्यास के प्रति लंबवत होती है।
इसलिए, दोनों कथन सही हैं।

MCQ: वृत्त - 1 - Question 11
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

एक वृत्त की एक तंतु की लंबाई वृत्त की त्रिज्या के बराबर है। यह तंतु वृत्त के बड़े खंड में जो कोण बनाता है वह बराबर है
Detailed Solution for MCQ: वृत्त - 1 - Question 11

AO = OB = AB
⇒ ∠AOB = 60° [∵ ΔAOB समबाहु त्रिकोण है]
नोट: वृत्त के केंद्र पर एक आर्क द्वारा बनाये गए कोण का मान उस आर्क के शेष भाग पर किसी भी बिंदु पर बनाये गए कोण के दोगुना होता है।
∴ ∠ACB = 30°
इसलिए, विकल्प A सही है।

MCQ: वृत्त - 1 - Question 12
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

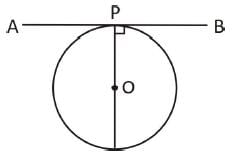
एक वृत्त (जिसका केंद्र O है) दो इंटरसेक्टिंग रेखाओं AX और BY को छू रहा है। संपर्क के दो बिंदु A और B वृत्त की परिधि पर किसी बिंदु C पर 65° का कोण बनाते हैं। यदि P दो रेखाओं का इंटरसेक्शन पॉइंट है, तो ∠APO का माप क्या होगा?
Detailed Solution for MCQ: वृत्त - 1 - Question 12

दी गई, ∠ACB = 65°
नोट: एक वृत्त के केंद्र पर एक आर्क द्वारा बनता कोण, उसके शेष भाग पर किसी भी बिंदु पर बनते कोण का दुगना होता है।
इसलिए, ∴ ∠AOB = 2 × 65° = 130°
नोट: वृत्त के किसी भी बिंदु पर एक टेन्जेंट उस बिंदु पर संपर्क बिंदु के माध्यम से व्यास के विपरीत होता है।
इसलिए, ∴ ∠OAP = 90°

हमें ज्ञात है कि, एक त्रिकोण के तीन कोणों का योग 180° है।
इसलिए, ∠APO = 180° – 90° – 65° = 25°
इसलिए, विकल्प A सही है।

MCQ: वृत्त - 1 - Question 13
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

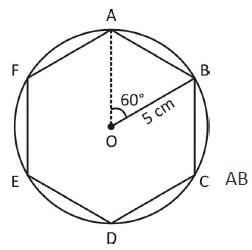
एक नियमित षट्भुज को 5 सेमी के त्रिज्या वाले वृत्त में अंकित किया गया है। यदि x वह क्षेत्र है जो वृत्त के अंदर है लेकिन नियमित षट्भुज के बाहर है, तो निम्नलिखित में से कौन सा सही है?
Detailed Solution for MCQ: वृत्त - 1 - Question 13

OB = OA = त्रिज्या

और ∠OAB = ∠OBA = 60° इसलिए, ΔAOB एक समसमान त्रिकोण है। तब, AB = 5 सेमी
इसलिए, क्षेत्र, x = वृत्त का क्षेत्र - षट्भुज का क्षेत्र

इसलिए, विकल्प A सही है।

MCQ: वृत्त - 1 - Question 14
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

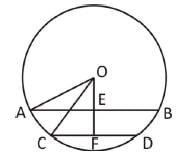
AB = 8 सेमी और CD = 6 सेमी दो समानांतर तंतु हैं जो वृत्त के केंद्र की एक ही तरफ हैं। उनके बीच की दूरी 1 सेमी है। वृत्त की त्रिज्या क्या है?
Detailed Solution for MCQ: वृत्त - 1 - Question 14

दी गई जानकारी के अनुसार, तंतु AB = 8 सेमी और CD = 6 सेमी है।
तब, AE = EB = 4 सेमी और CF = FD = 3 सेमी
EF = 1 सेमी
मान लीजिए OE = x सेमी है।
फिर, OF = (x + 1) सेमी है।
OA = OC = r सेमी (त्रिज्या)
ΔOAE से, पायथागोरस प्रमेय के अनुसार।

ΔOCF से, पायथागोरस प्रमेय के अनुसार।

संकेत (ii) - (i) द्वारा,

इस प्रकार, संकेत (i) से,
9 = r2 - 16
⇒ r2 = 25
⇒ r = 5 सेमी
इसलिए, विकल्प A सही है।

MCQ: वृत्त - 1 - Question 15
Save

निर्देश: कृपया निम्नलिखित प्रश्न को ध्यान से पढ़ें और सही उत्तर चुनें:

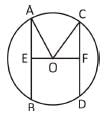
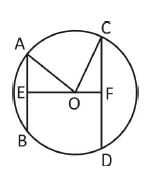
AB और CD दो समानांतर रेखाएं हैं जो वृत्त के केंद्र के विपरीत पक्षों पर हैं। यदि AB = 10 सेमी, CD = 24 सेमी और वृत्त की त्रिज्या 13 सेमी है, तो रेखाओं के बीच की दूरी क्या है?
Detailed Solution for MCQ: वृत्त - 1 - Question 15

दी गई जानकारी के अनुसार, रेखाएं AB = 10 और CD = 24 सेमी हैं।
∴ AE = EB = 5 सेमी और CF = FD = 12 सेमी
त्रिज्या AO = OC = 13 सेमी है।
ΔAOE से, पायथागोरस प्रमेय के अनुसार

और ΔCOF से, पायथागोरस प्रमेय के अनुसार

इसलिए, विकल्प A सही है।

142 videos|172 docs|185 tests
Join Course
Information about MCQ: वृत्त - 1 Page
In this test you can find the Exam questions for MCQ: वृत्त - 1 solved & explained in the simplest way possible. Besides giving Questions and answers for MCQ: वृत्त - 1, EduRev gives you an ample number of Online tests for practice
142 videos|172 docs|185 tests
Join Course
Download as PDF

Important Questions for MCQ: वृत्त - 1

Find all the important questions for MCQ: वृत्त - 1 at EduRev.Get fully prepared for MCQ: वृत्त - 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the MCQ: वृत्त - 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of MCQ: वृत्त - 1 resources.

MCQ: वृत्त - 1

Prepare for the MCQ: वृत्त - 1 within the RRB NTPC/ASM/CA/TA exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for MCQ: वृत्त - 1 Mathematics for RRB NTPC (Hindi)

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace MCQ: वृत्त - 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily