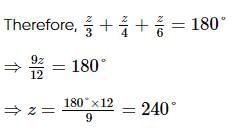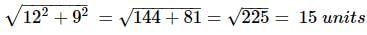MCQ: Coordinate Geometry - 2 - SSC CGL MCQ
15 Questions MCQ Test - MCQ: Coordinate Geometry - 2
If the points A(4, 3)and B(x, 5) are on the circle with Centre O (2, 3). Find the value of x.
If the distance between two points (0, -5) and (x,0) is 13 unit, then x equals to -
The equation of the line passing through (1, 2) and parallel to 3x + 4y + 7 = 0.
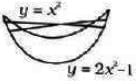
Suppose R is the region bounded by the two curves y = x2 and y = 2x2 − 1 as shown in the following diagram
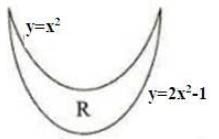
Two distinct lines are drawn such that each of these lines partitions the regions into at least two parts. If 'n' is the total number of regions generated by these lines, then
Find the distance between the points (−5,7) and (−1,3).
The point of intersection of the line x + y + 1 = 0 and 2x – y + 5 = 0 is
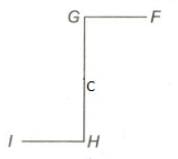
In the diagram AB || GH || DE and GF || BD || HI, ∠FGC = 80o, find the value of ∠CHI.

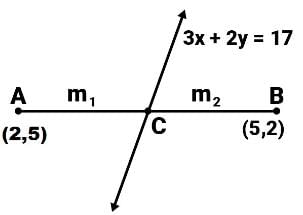
Find the ratio in which line 3x + 2y = 17 divides the line segment joined by points (2,5) and (5,2).
Let the vertices of a triangle ABC be (4, 4), (3, 5) and (−1,−1), then the triangle is:
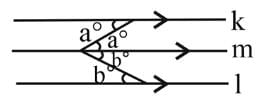
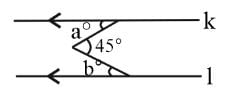
On the figure below, lines k and l are ∥.
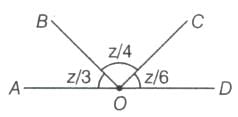
The value of a° + b° is _______.
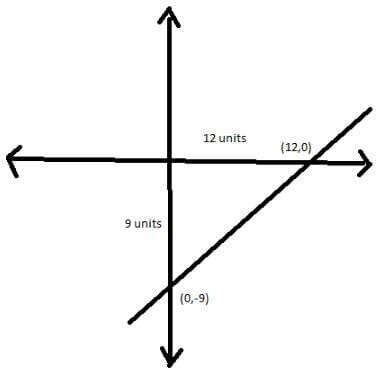
The length of the intercept of the graph of the equation 9x − 12y = 108 between the two axis is -


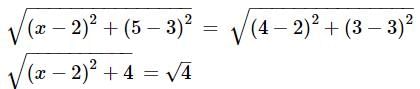
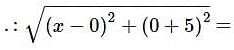 13
13
 What is the value of a?
What is the value of a?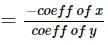
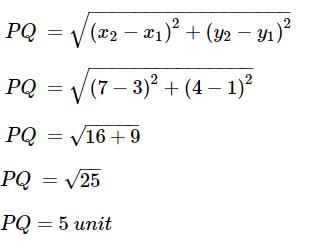
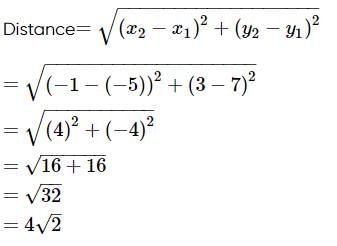
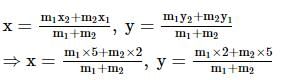
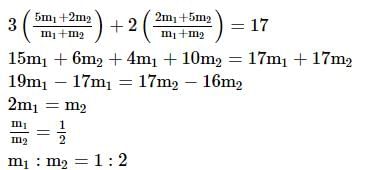
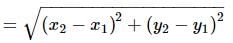
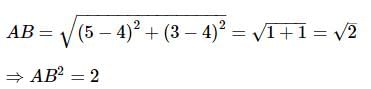
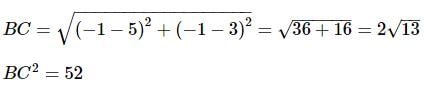
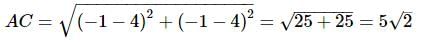
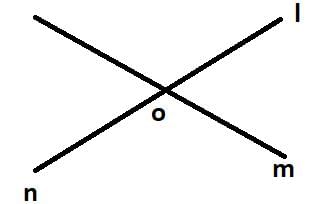
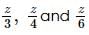 form a linear pair.
form a linear pair.