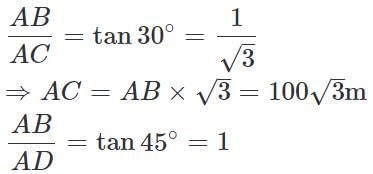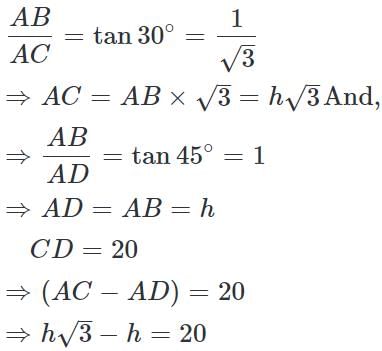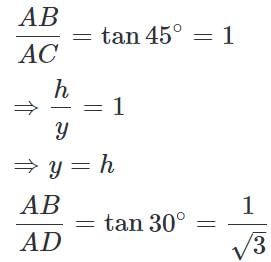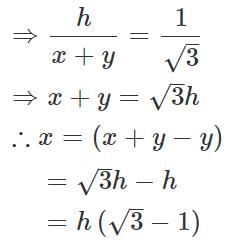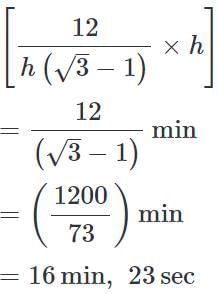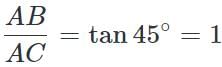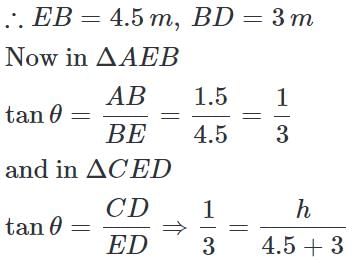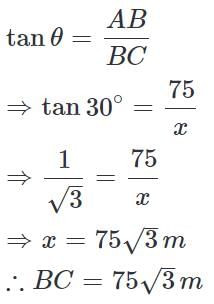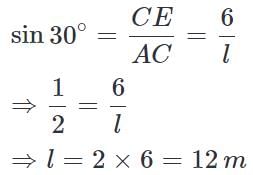All Courses
Get the App Signup / Login
Sign in Open App
Bank Exams Exam  >  Bank Exams Tests  >  Numerical Ability for Banking Exams  >  MCQ Test: Height and Distance- 1 - Bank Exams MCQ

MCQ Test: Height and Distance- 1 - Bank Exams MCQ


Test Description

20 Questions MCQ Test Numerical Ability for Banking Exams - MCQ Test: Height and Distance- 1

MCQ Test: Height and Distance- 1 for Bank Exams 2024 is part of Numerical Ability for Banking Exams preparation. The MCQ Test: Height and Distance- 1 questions and answers have been prepared according to the Bank Exams exam syllabus.The MCQ Test: Height and Distance- 1 MCQs are made for Bank Exams 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for MCQ Test: Height and Distance- 1 below.
Solutions of MCQ Test: Height and Distance- 1 questions in English are available as part of our Numerical Ability for Banking Exams for Bank Exams & MCQ Test: Height and Distance- 1 solutions in Hindi for Numerical Ability for Banking Exams course. Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free. Attempt MCQ Test: Height and Distance- 1 | 20 questions in 20 minutes | Mock test for Bank Exams preparation | Free important questions MCQ to study Numerical Ability for Banking Exams for Bank Exams Exam | Download free PDF with solutions
MCQ Test: Height and Distance- 1 - Question 1
Save

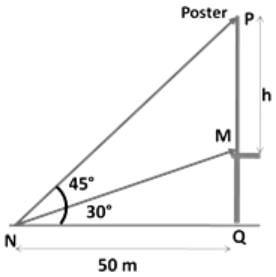
A poster is on top of a building. Rajesh is standing on the ground at a distance of 50 m from the building. The angles of elevation to the top of the poster and bottom of the poster are 45° and 30° respectively. What is the height of the poster?

Detailed Solution for MCQ Test: Height and Distance- 1 - Question 1


In ΔPNQ, Tan 45° = PQ/NQ
∴ PQ = NQ = 50m
In ΔMNQ, Tan 30° = MQ/NQ

∴ h = PM = PQ - MQ = 50 - 50/√3 = 50/√3 (√3 - 1) = Poster height

MCQ Test: Height and Distance- 1 - Question 2
Save

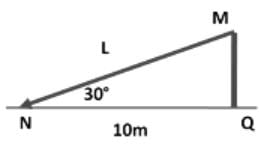
A tree is cut partially and made to fall on ground. The tree however does not fall completely and is still attached to its cut part. The tree top touches the ground at a point 10m from foot of the tree making an angle of 30°. What is the length of the tree?

Detailed Solution for MCQ Test: Height and Distance- 1 - Question 2


In ΔMNQ, Tan 30° = MQ/NQ
∴ 1/√3 = MQ/10
∴ MQ = 10/√3
Also, By Pythagoras theorem,
MN2 = MQ2 + NQ2
∴ L2 = 100/3 + 100
∴ L = 20/√3
∴ Height of tree = L + MQ 

1 Crore+ students have signed up on EduRev. Have you? Download the App
MCQ Test: Height and Distance- 1 - Question 3
Save

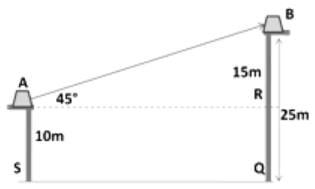
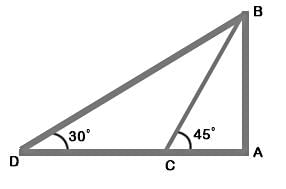
Two houses are in front of each other. Both have chimneys on their top. The line joining the chimneys makes an angle of 45° with the ground. How far are the houses from each other if one house is 25m and other is 10m in height?

Detailed Solution for MCQ Test: Height and Distance- 1 - Question 3


In ΔABR, a ∠ARB = 90° and ∠BAR = 45°
Sum of angles of a triangle = 180°
So ∠ABR = 180-90-90 = 45°
∴ BR = AR
AS = RQ = 10m
Also, BR = BQ-RQ = 25-10 = 15m
∴ AR = 15m = Distance between houses

MCQ Test: Height and Distance- 1 - Question 4
Save

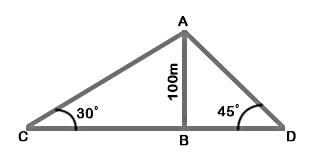
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 4

Then, AB = 100m, ∠ACB = 30° and ∠ADB = 45°

⇒ AD = AB = 100m
∴ CD = (AC+AD) = (100√3 +100)
= 100(√3 +1) = 100(1.73+1) =100 × 2.73 = 273m

MCQ Test: Height and Distance- 1 - Question 5
Save

The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 5

Let AB be the wall and BC be the ladder.

Then, ∠ACB = 60° = AC = 4.6m
AC/BC = cos 60° = 1/2
⇒ BC = 2 × AC = 2 × 4.6 = 9.2m

MCQ Test: Height and Distance- 1 - Question 6
Save

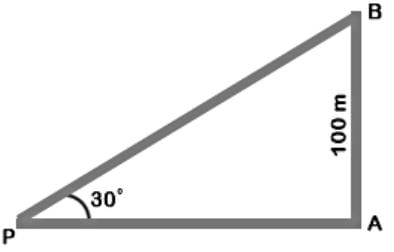
From a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 100 m high, the distance of point P from the foot of the tower is:
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 6

Let AB be the tower.

Then, ∠APB = 30° and AB = 100m
AB/AP = tan 30° = 1/√3
⇒ AP = AB × √3 = 100 × √3
⇒ AP = 100 × 1.73 = 173m

MCQ Test: Height and Distance- 1 - Question 7
Save

The angle of elevation of the top of a tower from a certain point is 30°. If the observed moves 20 m towards the tower, the angle of elevation the angle of elevation of top of the tower increases by 15°. The height of the tower is
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 7


Let AB be the tower and C and D be the points of observation.
Then, ∠ACB = 30°, ∠ADB = 45° and CD = 20m
Let AB = h then,

MCQ Test: Height and Distance- 1 - Question 8
Save

A man on the top of a vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower ?
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 8


Let AB be the tower and C and D be the two positions of the car.
Then, ∠ACB = 45∘, ∠ADB = 30∘
Let, AB = h, CD = x and AC = y


Now, h (√3 - 1) is covered in 12 min.
So, h will be covered in→

MCQ Test: Height and Distance- 1 - Question 9
Save

If a 30 m ladder is placed against a 15 m wall such that it just reaches the top of the wall, then the elevation of the wall is equal to-
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 9


AC = 30 meter
AB = 15 meter
∠ACB = θ

MCQ Test: Height and Distance- 1 - Question 10
Save

A boy is standing at the top of the tower and another boy is at the ground at some distance from the foot of the tower, then the angle of elevation and depression between the boys when both look at a each other will be-
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 10


Here, AD is parallel to BC and AC is a transversal.
⇒ θ1 = θ2

MCQ Test: Height and Distance- 1 - Question 11
Save

A man is watching from the top of tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man’s eye when at a distance of 60 meters from the tower. After 5 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 11


Let AB be the tower and C and D be the two positions of the boats.
Then, ∠ACB = 45∘, ∠ADB = 30∘ and AC = 60 m
Let, AB = h
Then,


Hence, required speed

MCQ Test: Height and Distance- 1 - Question 12
Save

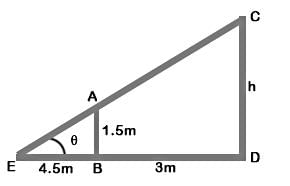
If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 12

Let AB is girls and CD is lamp-post AB = 1.5
which casts her shadow EB


MCQ Test: Height and Distance- 1 - Question 13
Save

Directions: Study the following questions carefully and choose the right answer:

The shadow of a tower is 15 m when the sun’s elevation is 30°. What is the length of the shadow when the sun’s elevation is 60°?
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 13


Given, ∠ADB = 30° and ∠ ACB = 60°

When the sun's elevation is 30°, the shaadow of tower is "BD = 15 m" and when the sun's elevation is 60°, the shadow of tower is "BC = ?"
Let, BC = x m
In ΔABD, tan 30° = AB/BD
1 / √3 = AB / 15
∴ AB = 15 / √3                           ....(i)
In ΔABC, tan 60° = AB/BC
√3 = AB / x
∴ AB = x √3        ...(ii)
From Eqs. (i) and (ii), we get
x√3 = 15 / √3
x = 5 m
Hence, optjon C is correct.

MCQ Test: Height and Distance- 1 - Question 14
Save

Directions: Study the following questions carefully and choose the right answer:

From the top of a cliff 90 m high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°, respectively. What is the height of the tower?
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 14


Given, AB = 90 m
∠ADE = 30°
And ∠ACB = 60°
Then, DC = ?
Ratio of angles,
tan 30º / tan 60º = (AE / ED) / (AB / BC)
[∵ ED = BC]
(1 / √3) / √3 = AE / 90
1 / 3 = AE / 90
AE = 30 m
Now, DC = EB
= AB – AE
= 90 – 30 = 60 m
Hence, option C is correct.

MCQ Test: Height and Distance- 1 - Question 15
Save

Directions: Study the following questions carefully and choose the right answer:

A telegraph post gets broken at a point against a storm and its top touches the ground at a distance 20 m from the base of the post making an angle 30° with the ground. What is the height of the post?
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 15


Given, BC = 20 m
∠ACB = 30°
Total height of the telegraph post is (AB + CA) = ?
In Δ ABC, tan 30° =  AB / BC
1 / √3 = AB / 20
∴ AB = 20 / √3m
Now, cos 30º = BC / AC
√3 / 2 = 20 / AC
∴ AC = 40 /√3 m
So, AB + CA = (20 / √3) + (40 / √3) = (60 / √3)
= 20 √3 m
Hence, option B is correct.

MCQ Test: Height and Distance- 1 - Question 16
Save

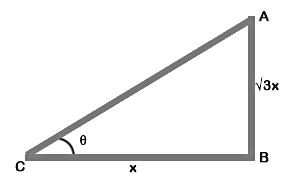
If the height of a vertical pole is √3 times the length of its shadow on the ground, then the angle of elevation of the sun at that time is
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 16

Let AB be a vertical pole and let its shadow be BC

Let BC = x m, then length of pole = √3x,
θ be the angle of elevation

MCQ Test: Height and Distance- 1 - Question 17
Save

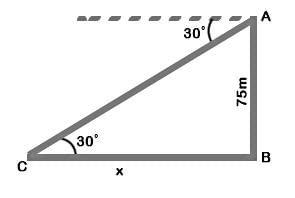
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 17

AB is a tower and AB = 75 m
From A, the angle of depression of a car C
on the ground is 30°

Let distance BC = x
Now in right ΔACB,

MCQ Test: Height and Distance- 1 - Question 18
Save

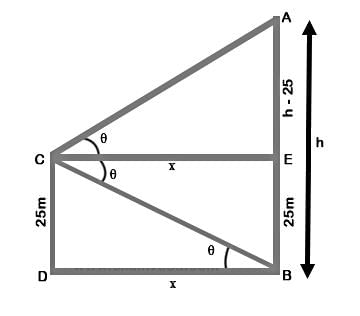
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 18

Let AB be the tower and CD be cliff Angle of elevation of A is equal to the angle of depression of B at C
Let angle be Q and CD = 25 m

Let AB = h
CE || DB
∴ EC = DB = x (suppose)
EB = CD = 25
∴ AE = h − 25
Now in right ΔCDB,

MCQ Test: Height and Distance- 1 - Question 19
Save

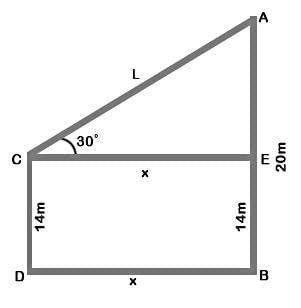
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 19

Let AB and CD be two poles
AB = 20 m, CD = 14 m
A and C are joined by a wire
CE || DB and angle of elevation of A is 30°
Let CE = DB = x and AC = L

Now AE = AB - EB = AB - CD = 20 - 14 = 6 m
Now in right ΔACE,

MCQ Test: Height and Distance- 1 - Question 20
Save

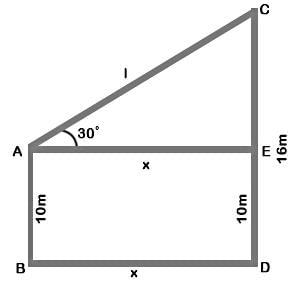
The tops of two poles of height 16 m and 10 m are connected by a wire of length l metres. If the wire makes an angle of 30° with the horizontal, then l =
Detailed Solution for MCQ Test: Height and Distance- 1 - Question 20

Let AB and CD are two poles AB = 10 m and CD = 16 m

AC is wire which makes an angle of 30° with the horizontal
Let BD = x, then AE = x
CE = CD - ED = CD - AB = 16 - 10 = 6m
Now in ΔACE

162 videos|119 docs|92 tests
Join Course
Information about MCQ Test: Height and Distance- 1 Page
In this test you can find the Exam questions for MCQ Test: Height and Distance- 1 solved & explained in the simplest way possible. Besides giving Questions and answers for MCQ Test: Height and Distance- 1, EduRev gives you an ample number of Online tests for practice

Top Courses for Bank Exams

Download as PDF

Top Courses for Bank Exams

Important Questions for MCQ Test: Height and Distance- 1

Find all the important questions for MCQ Test: Height and Distance- 1 at EduRev.Get fully prepared for MCQ Test: Height and Distance- 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the MCQ Test: Height and Distance- 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of MCQ Test: Height and Distance- 1 resources.

MCQ Test: Height and Distance- 1

Prepare for the MCQ Test: Height and Distance- 1 within the Bank Exams exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for MCQ Test: Height and Distance- 1 Numerical Ability for Banking Exams

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace MCQ Test: Height and Distance- 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup