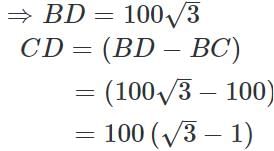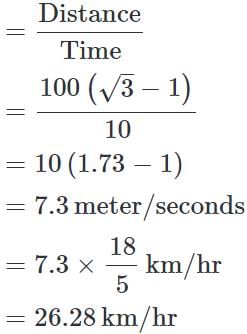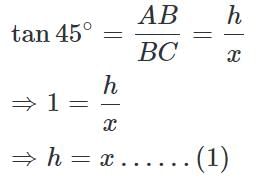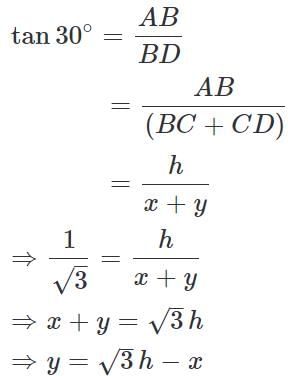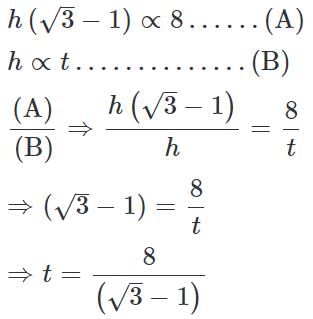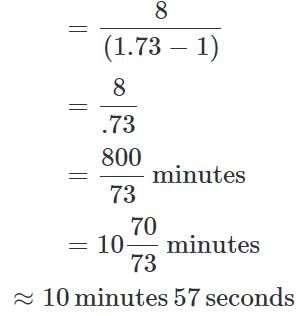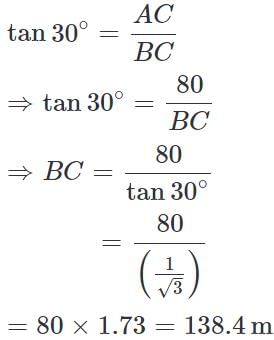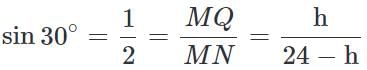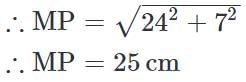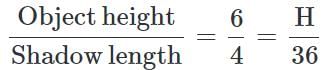MCQ Test: Height and Distance- 2 - Bank Exams MCQ
20 Questions MCQ Test Numerical Ability for Banking Exams - MCQ Test: Height and Distance- 2
Directions: Study the following questions carefully and choose the right answer:
The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many metres?
Directions: Study the following questions carefully and choose the right answer:
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 200 m apart, find the height of the light house.
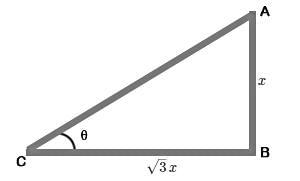
The length of shadow of a tower on the plane ground is √3 times the height of the tower. The angle of elevation of sun is
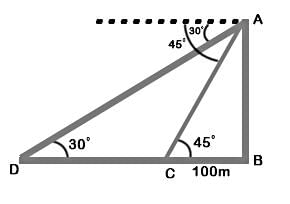
The angle of elevation of the top of a lighthouse 60 m high, from two points on the ground on its opposite sides are 45° and 60°. What is the distance between these two points?
On the same side of a tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 600 m, the distance between the objects is approximately equal to:
Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30º and 45º respectively. If the lighthouse is 200 m high, the distance between the two ships is:
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 40 m towards the tower, the angle of elevation of the top of the tower increases by 15°. The height of the tower is:
The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 12.4 m away from the wall. The length of the ladder is:
A vertical tower stands on ground and is surmounted by a vertical flagpole of height 18 m. At a point on the ground, the angle of elevation of the bottom and the top of the flagpole are 30° and 60° respectively. What is the height of the tower?
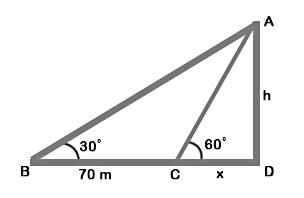
When the sun's altitude changes from 30° to 60°, the length of the shadow of a tower decreases by 70m. What is the height of the tower?
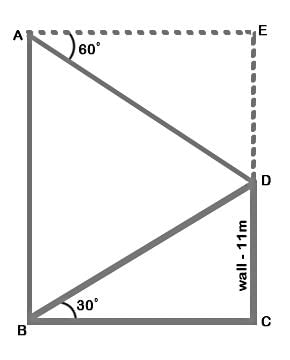
The angles of depression and elevation of the top of a wall 11 m high from top and bottom of a tree are 60° and 30° respectively. What is the height of the tree?
A man is watching from the top of a tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man's eye when at a distance of 100 metres from the tower. After 10 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?
The angle of elevation of the sun, when the length of the shadow of a tree is equal to the height of the tree, is:
A man on the top of a vertical observation tower observers a car moving at a uniform speed coming directly towards it. If it takes 8 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower?
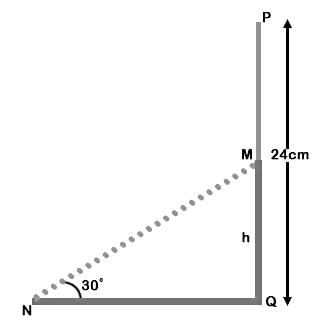
From a tower of 80 m high, the angle of depression of a bus is 30°. How far is the bus from the tower?
A tree breaks and falls to the ground such that its upper part is still partially attached to its stem. At what height did it break, if the original height of the tree was 24 cm and it makes an angle of 30° with the ground?
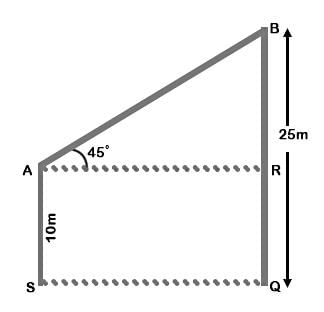
Two houses are in front of each other. Both have chimneys on their top. The line joining the chimneys makes an angle of 45° with the ground. How far are the houses from each other if one house is 25m and other is 10m in height?
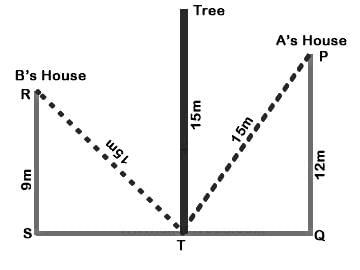
There is a tree between houses of A and B. If the tree leans on A’s House, the tree top rests on his window which is 12 m from ground. If the tree leans on B’s House, the tree top rests on his window which is 9 m from ground. If the height of the tree is 15 m, what is distance between A’s and B’s house?
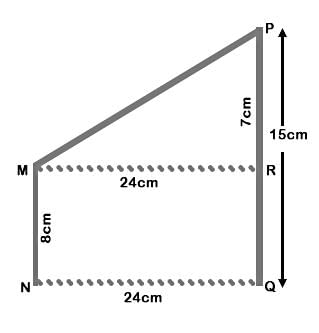
Ramesh and Suresh’s mud forts have heights 8 cm and 15 cm. They are 24 cm apart. How far are the fort tops from each other?
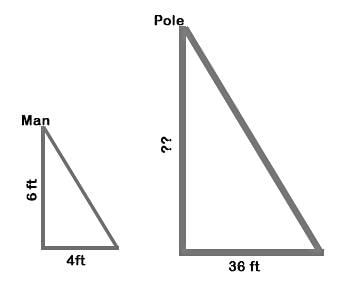
Due to sun, a 6ft man casts a shadow of 4ft, whereas a pole next to the man casts a shadow of 36ft. What is the height of the pole?
|
167 videos|158 docs|92 tests
|






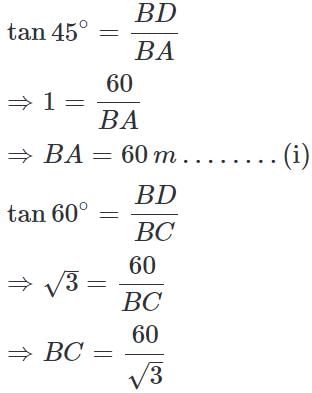
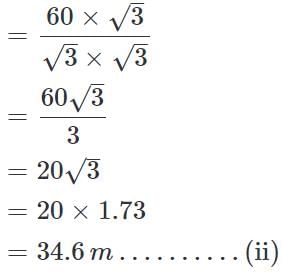
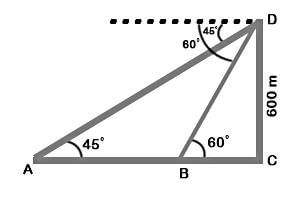
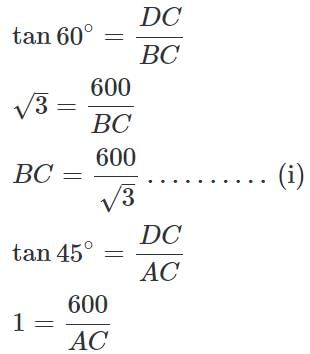
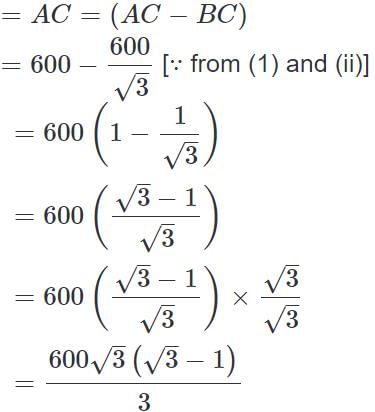
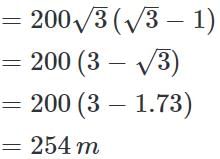
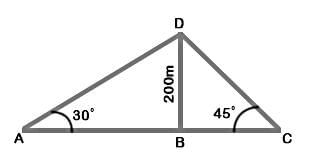
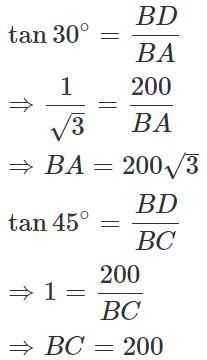
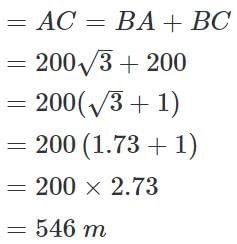
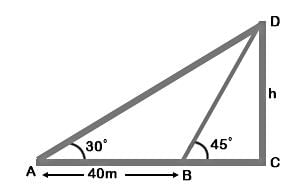
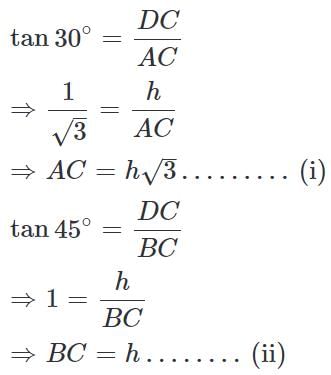
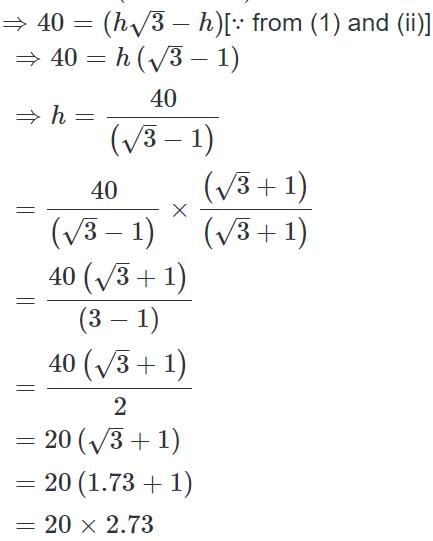
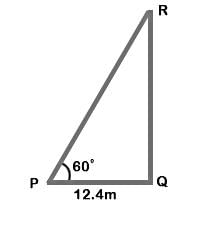
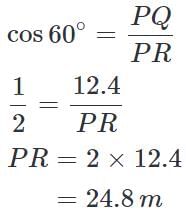
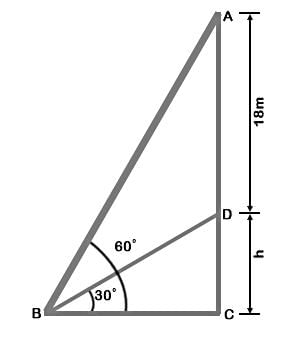
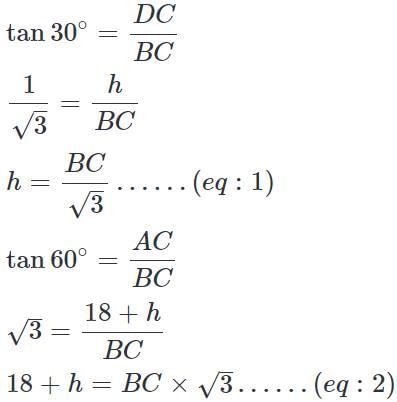
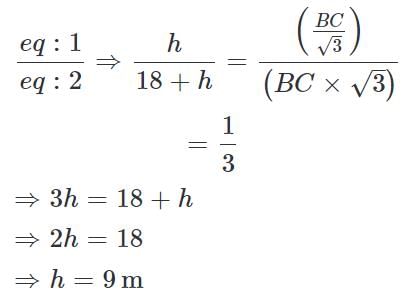


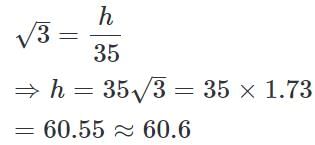


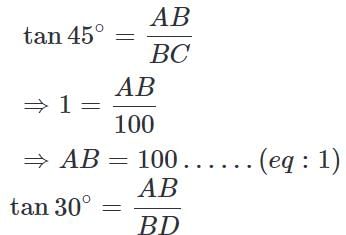
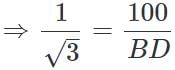 (∵ Substituted the value of AB from equation 1)
(∵ Substituted the value of AB from equation 1)