MCQ Test: Linear Inequalities - Bank Exams MCQ
15 Questions MCQ Test Reasoning Aptitude for Competitive Examinations - MCQ Test: Linear Inequalities
If x2 - 6x - 27 > 0, then which one of the following is correct?
If 2(3x - 4) - 2 < 4x - 2 ≥ 2x - 4; then the possible value of x can be:
The equations ax + 9y = 1 and 9y - x - 1 = 0 represent the same line if a =
For what value of 'a', does the inequality 9a - a2 ≤ 17a + 15 holds
Calculate the least whole number, which when subtracted from both the terms of the ratio 5 : 6 gives a ratio less than 17 : 22.
Find out the relation between x and y
I. x² - 5x + 6 = 0
II. y² - 9y + 20 = 0
Given, 6x + 2(6 - x) > 2x - 2 < 5x/2 - 3x/4, then x can take which of the following values?
If a + b = 5 and 2a – b = 4. Find the relation between a and b.
If 2x + 5 > 2 + 3x and 2x - 3 ≤ 4x - 5, then x can take which of the following values?
If a2 - b2 = 88, a - b = 4 then find the value of ab.
If 3x + 4(1 – x) > 5x – 2 > 3x – 4; then the value of x is
If 4(x + 5) - 3 > 6 - 4x ≥ x - 5; Then the value of x is
|
11 videos|20 docs|171 tests
|
|
11 videos|20 docs|171 tests
|




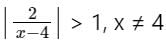
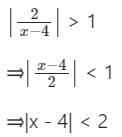
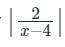 > 1 is x ϵ (4, 6).
> 1 is x ϵ (4, 6).