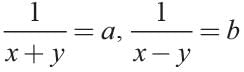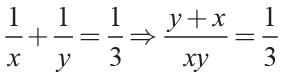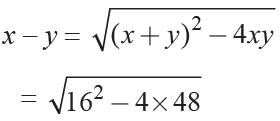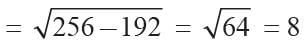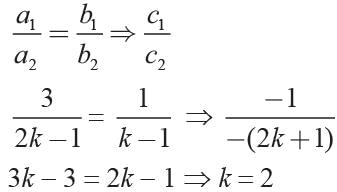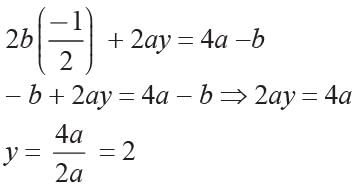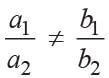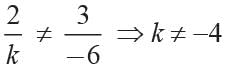Math Olympiad Test: Linear Equations in Two Variables- 1 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Linear Equations in Two Variables- 1
What are the values of x and y if
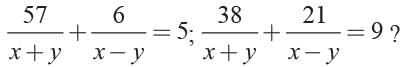
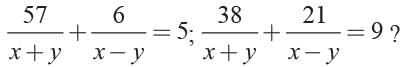
The sum of two numbers is 16 and the sum of their reciprocals is 1/3. What are the numbers?
In a triangle ΔABC, 3∠B = ∠C = 2 (∠A + ∠B). Which angle is the largest and what is its value?
What is the value of k for which the system of equations 3x + y = 1 and (2k - 1) x + (k - 1) y = 2k + 1 has no solution.
What are the values of x and y, if 2(ax - by) + (a + 4b) = 0 and 2 (bx + ay) + (b - 4a) = 0
The length of a field exceeds its breadth by 3 meters. If the length is increased by 3 meters and the breadth is decreased by 2 meters. The area remains the same. What are the length and breadth respectively of the field?
What is the value of k except which the given system of equations has a unique solution?
2x + 3y - 5 = 0 and kx - 6y - 8 = 0
Five years ago, Ravi was thrice as old as Shashi. Ten years later Ravi will be twice as old as Shashi. What is the age of Shashi?
In a cyclic quadrilateral ABCD, ∠A = 2x - 1, ∠B = y + 5, ∠C = 2y + 15, ∠D = 4x - 7. Which is the greatest angle of quadrilateral.
Rajesh scored 40 marks on a test getting 3 marks for each right answer and losing one mark for each wrong answer. If 4 marks have been awarded for each correct answer and 2 marks have been deducted for each incorrect answer then Rajesh will score 50 marks. What is the number of questions in the test?