Mathematics Test - 1 - SAT MCQ
30 Questions MCQ Test SAT Mock Test Series 2025 - Mathematics Test - 1
The nth term of a sequence is given by the expression bn + 4, where b is a positive constant. Which of the following is necessarily equal to b ?
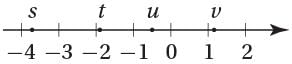
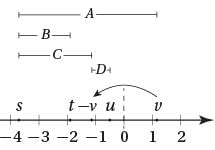
If s, t, u, and v are the coordinates of the indicated points on the number line above, which of the following is greatest?
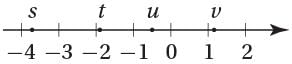
If s, t, u, and v are the coordinates of the indicated points on the number line above, which of the following is greatest?
If 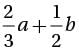 = 5, and b = 4, what is the value of α? (Give answer in decimal upto one digit after decimal.)
= 5, and b = 4, what is the value of α? (Give answer in decimal upto one digit after decimal.)
In a survey of 80 students, 55 students stated that they play a varsity sport, and 35 stated that they are taking at least one AP level course. Which of the following statements must be true?
Let function f(x) be defined by the equation f (x) = x2 - 1. If b is a positive real number, then f(1/b) =
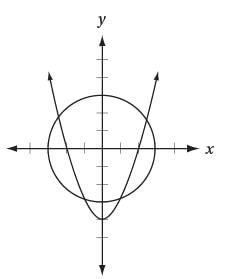
x2 + y2 = 9
y = x2 - 4
A system of two equations and their graphs in the xy-plane are shown above. How many solutions does the system have?
Line l intersects the graph of the function f(x) = 2x2 - 4x + 1 at two points where x = -1 and x = 2, respectively. What is the slope of line l?
What is the total number of x- and y-intercepts in the graph of the equation y = (x + 2)2(x - 3)2?
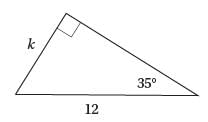
In the triangle above, what is the value of k? (sin 35° = 0.574, cos 35° = 0.819, tan 35° = 0.700)
The value of y varies with x according to the equation y = a(x - 2)(x + 1), where a < 0. As the value of x increases from 0 to 5, which of the following best describes the behavior of y?
Which of the following is equal to a2/3, for all values of a ?
The average number of students per classroom at Central High School from 2000 to 2010 can be modeled by the equation y = 0.56x + 27.2, where x represents the number of years since 2000, and y represents the average number of students per classroom. Which of the following best describes the meaning of the number 0.56 in the equation?
h =− 16t2 + vt + k
The equation above gives the height h, in feet, of a ball t seconds after it is thrown straight up with an initial speed of v feet per second from a height of k feet. Which of the following gives v in terms of h, t, and k ?
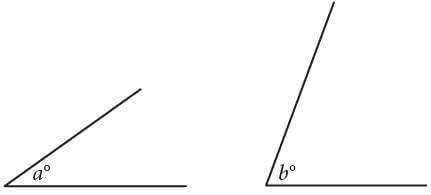
The angles shown above are acute and sin (α°) = cos (b°). If α = 4k − 22 and b = 6k − 13, what is the value of k ?
Which of the following is an example of a function whose graph in the xy-plane has no x-intercepts?
y = x2
2y + 6 = 2(x + 3)
If (x, y) is a solution of the system of equations above and x > 0, what is the value of xy?
f (x) = 2x + 1
The function f is defined by the equation above.
Which of the following is the graph of y = − f (x) in the xy-plane?
In the 1908 Olympic Games, the Olympic marathon was lengthened from 40 kilometers to approximately 42 kilometers. Of the following, which is closest to the increase in the distance of the Olympic marathon, in miles? (1 mile is approximately 1.6 kilometers.)
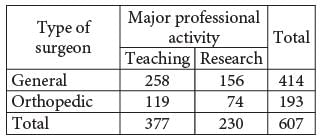
In a survey, 607 general surgeons and orthopedic surgeons indicated their major professional activity.
The results are summarized in the table above. If one of the surgeons is selected at random, which of the following is closest to the probability that the selected surgeon is an orthopedic surgeon whose indicated professional activity is research?
αx3 + bx2 + cx + d = 0
In the equation above, α, b, c, and d are constants.
If the equation has roots −1 , −3 , and 5, which of the following is a factor of αx3 + bx2 + cx + d?
The expression 1/3 x2 - 2 can be rewritten as 1/3 (x - k) (x + k), where k is a positive constant.What is the value of k ?
(7532 + 100y2) + 10(10y2 − 110)
The expression above can be written in the form αy2 + b , where α and b are constants. What is the value of α + b ?
Which of the following ordered pairs (x, y) satisfies the inequality 5x − 3y < 4 ?
I. (1, 1)
II. (2, 5)
III. (3, 2)
Lani spent 15% of her 8-hour workday in meetings. How many minutes of her workday did she spend in meetings?
Question refer to the following information.
Mosteller’s formula: A = 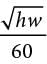
Current’s formula: A = 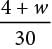
The formulas above are used in medicine to estimate the body surface area A, in square meters, of infants and children whose weight w ranges between 3 and 30 kilograms and whose height h is measured in centimeters.
Q. If Mosteller’s and Current’s formulas give the same estimate for A, which of the following expressions is equivalent to 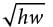 ?
?
|
8 docs|15 tests
|



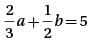
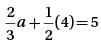
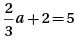
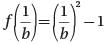
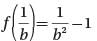
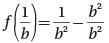
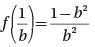
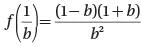
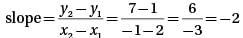
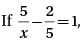 what is the value of x?
what is the value of x? 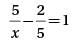
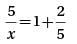

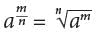 for any positive integers m and n. It follows, therefore, that
for any positive integers m and n. It follows, therefore, that 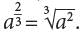
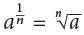 for any positive integer n.
for any positive integer n.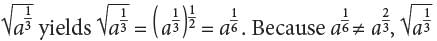 is not the correct answer. Choice B is incorrect. By definition,
is not the correct answer. Choice B is incorrect. By definition, 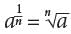 for any positive integer n.
for any positive integer n.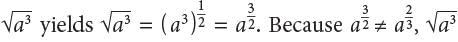 is not the correct answer. Choice C is incorrect. By definition,
is not the correct answer. Choice C is incorrect. By definition, 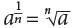 for any positive integer n. Applying this definition as well as the power property of exponents to the expression
for any positive integer n. Applying this definition as well as the power property of exponents to the expression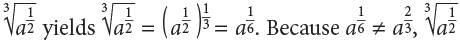 is not the correct answer.
is not the correct answer.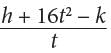 is not one of the options, so the right side needs to be further simplified. Another way to write the previous equation is
is not one of the options, so the right side needs to be further simplified. Another way to write the previous equation is 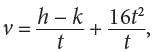 which can be simplified to v =
which can be simplified to v = 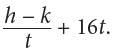
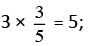 however, 9/5 is not equal to 5.
however, 9/5 is not equal to 5. 

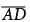 ?
?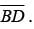 In triangle ADB, side
In triangle ADB, side 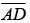 is opposite to the angle 30°; therefore, the length of
is opposite to the angle 30°; therefore, the length of 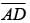 is half the length of hypotenuse
is half the length of hypotenuse 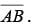 Since the triangles are congruent, AB = BC = 12. So the length of
Since the triangles are congruent, AB = BC = 12. So the length of 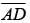 is 12/2 = 6.
is 12/2 = 6.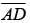 were 4, then the length of
were 4, then the length of 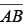 would be 8. However, this is incorrect because
would be 8. However, this is incorrect because 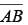 is congruent to
is congruent to 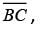 which has a length of 12. Choices C and D are also incorrect. Following the same procedures as used to test choice A gives
which has a length of 12. Choices C and D are also incorrect. Following the same procedures as used to test choice A gives 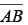 a length of 12√2 for choice C and 12√3 for choice D. However, these results cannot be true because AB is congruent to
a length of 12√2 for choice C and 12√3 for choice D. However, these results cannot be true because AB is congruent to 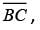 which has a length of 12.
which has a length of 12.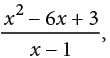 what is f(−1) ?
what is f(−1) ?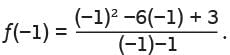 Simplifying the expressions in the numerator and denominator yields
Simplifying the expressions in the numerator and denominator yields which is equal to 10/-2 or –5.
which is equal to 10/-2 or –5.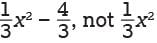 − 2. Choice B is incorrect. This may result from incorrectly factoring the expression and finding (x – 6) (x + 6) as the factored form of the expression. Choice C is incorrect. This may result from incorrectly distributing the 1/3 and rewriting the expression as 1/3 (x2 − 2).
− 2. Choice B is incorrect. This may result from incorrectly factoring the expression and finding (x – 6) (x + 6) as the factored form of the expression. Choice C is incorrect. This may result from incorrectly distributing the 1/3 and rewriting the expression as 1/3 (x2 − 2).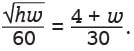
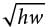 gives
gives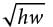 =
= 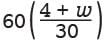 or
or 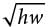 = 2(4 + w).
= 2(4 + w).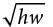 is equivalent to 2(4 + w).
is equivalent to 2(4 + w).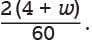
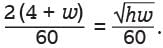
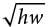 = 2(4 + w).
= 2(4 + w).










