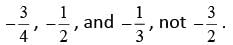Mathematics Test - 3 - SAT MCQ
30 Questions MCQ Test - Mathematics Test - 3

If the area of the figure above is 16/5 square units, what is its perimeter?

If the area of the figure above is 16/5 square units, what is its perimeter?
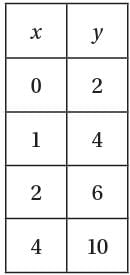
Based on the ordered pairs in the table above, which of the following could express a relationship between x and y ?
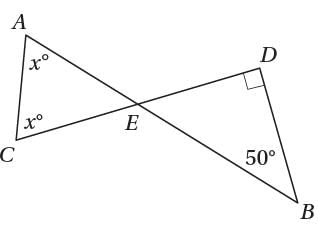
In the figure above, line segments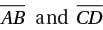 intersect at point E. What is the value of x ?
intersect at point E. What is the value of x ?
Everyone in Niko’s class has a different birth date. If Niko is both the 8th oldest person and the 12th youngest person in his class, how many students are in Niko’s class?
The functions f, g, and h are defined by the equations f (x) = x2, g (x) = x, and h(x) = √x. Which of the following must be true?
If the function f is defined by the equation f(x) = k(x + 6)(x − 1), where k > 5, t hen which of t he following is equivalent to f(7) ?
If the function m(x) satisfies the equation 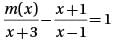 for all values of x greater than 1, then m(x) =
for all values of x greater than 1, then m(x) =
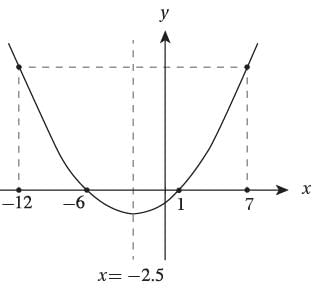
If k > 2, which of the following could be the graph of y + x = k(x - 1) in the x y-plane?
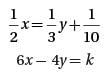
For what value of k will the system of equations above have at least one solution?
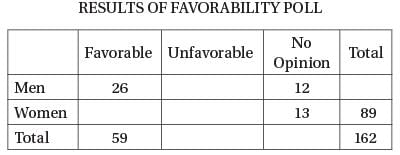
The table above shows the partial results of a favorability poll for a local politician. If the data shown are correct, how many of the women who were polled viewed the politician unfavorably?
Question based on the graph below.
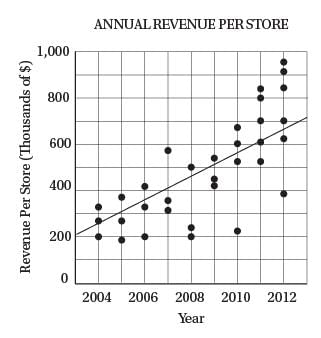
The scatterplot above shows the annual revenue for each of the individual retail stores operated by a clothing company for each year from 2004 through 2012. Based on the line of best fit to the data shown, which of the following is closest to the average annual increase in revenue per store?
A culture of bacteria initially contained p cells, where p > 100. After one hour, this population decreased by 1/3. In the second and third hours, however, the population increased by 40% and 50%, respectively. At the end of those first three hours, what was the population of the culture?
The variables x and y are believed to correlate according to the equation y = ax2 + bx + c, where a, b, and c are constants. Which of the following scatterplots would provide the strongest evidence in support of the hypothesis that a < 0?
An online trading company charges a 3% commission for all stock purchases. If a trader purchases 200 shares of a stock through this company and is charged $3,399 including commission, what is the cost per share for this stock?
In the xy-plane, the parabola with equation y = (x − 11)2 intersects the line with equation y = 25 at two points, A and B. What is the length of 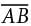 ?
?
C = 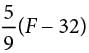
The equation above shows how a temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?
I. A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 5/9 degree Celsius.
II. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
III. A temperature increase of 5/9 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.
In triangle ABC, the measure of ∠B is 90° , BC = 16 , and AC = 20. Triangle DEF is similar to triangle ABC, where vertices D, E, and F correspond to vertices A, B, and C, respectively, and each side of triangle DEF is 1/3
the length of the corresponding side of triangle ABC. What is the value of sin F?
At Lincoln High School, approximately 7 percent of enrolled juniors and 5 percent of enrolled seniors were inducted into the National Honor Society last year. If there were 562 juniors and 602 seniors enrolled at Lincoln High School last year, which of the following is closest to the total number of juniors and seniors at Lincoln High School last year who were inducted into the National Honor Society?
Question refer to the following information.
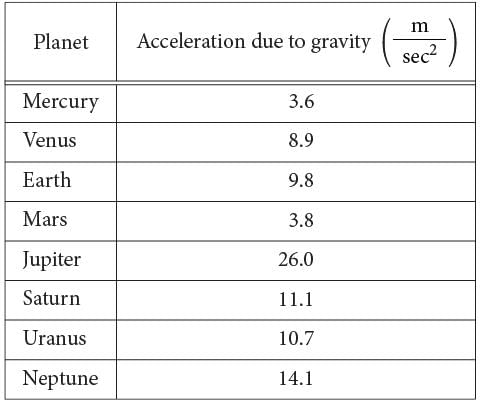
The chart above shows approximations of the acceleration due to gravity in meters per second squared 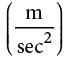 for the eight planets in our solar system. The weight of an object on a given planet can be found by using the formula W =mg , where W is the weight of the object measured in newtons, m is the mass of the object measured in kilograms, and g is the acceleration due to gravity on the planet measured in m/sec2.
for the eight planets in our solar system. The weight of an object on a given planet can be found by using the formula W =mg , where W is the weight of the object measured in newtons, m is the mass of the object measured in kilograms, and g is the acceleration due to gravity on the planet measured in m/sec2.
Q. What is the weight, in newtons, of an object on Mercury with a mass of 90 kilograms?
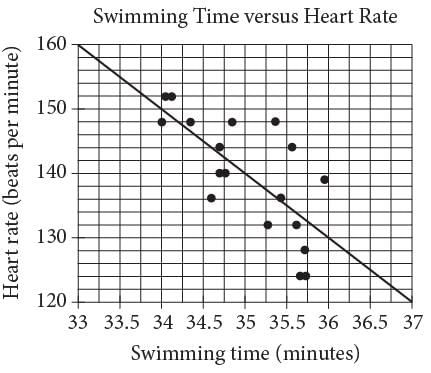
Michael swam 2,000 yards on each of eighteen days.
The scatterplot above shows his swim time for and corresponding heart rate after each swim. The line of best fit for the data is also shown. For the swim that took 34 minutes, Michael’s actual heart rate was about how many beats per minutes less than the rate predicted by the line of best fit?
The volume of right circular cylinder A is 22 cubic centimeters. What is the volume, in cubic centimeters, of a right circular cylinder with twice the radius and half the height of cylinder A?
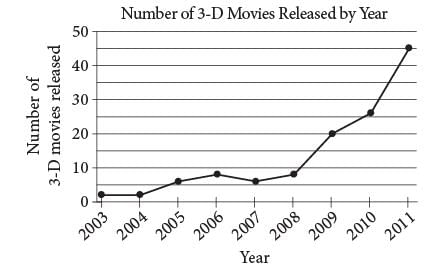
According to the line graph above, between which two consecutive years was there the greatest change in the number of 3‑D movies released?
−2x + 3y = 6
In the xy-plane, the graph of which of the following equations is perpendicular to the graph of the equation above?
x = y - 3
x/2 + 2y = 6
Which ordered pair (x, y) satisfies the system of equations shown above?
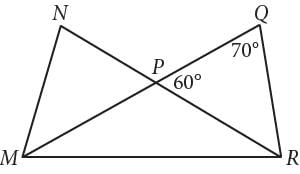
In the figure above, 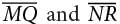 intersect at point P, NP = QP , and MP = PR. What is the measure, in degrees, of ∠ QMR ? (Disregard the degree symbol when gridding your answer.)
intersect at point P, NP = QP , and MP = PR. What is the measure, in degrees, of ∠ QMR ? (Disregard the degree symbol when gridding your answer.)
A customer paid $53.00 for a jacket after a 6 percent sales tax was added. What was the price of the jacket before the sales tax was added?
y = 19.99 + 1.50x
The equation above models the total cost y,in dollars, that a company charges a customer to rent a truck for one day and drive the truck x miles. The total cost consists of a flat fee plus a charge per mile driven. When the equation is graphed in the xy-plane, what does the y-intercept of the graph represent in terms of the model?


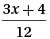 ?
?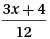
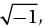 which of t he follow ing is NOT equal to i3 + i ?
which of t he follow ing is NOT equal to i3 + i ?
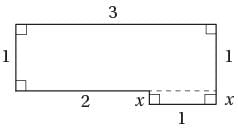
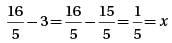
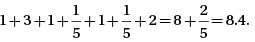
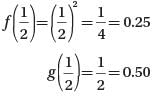
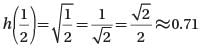
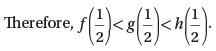
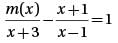
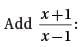
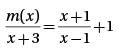
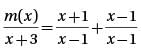
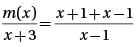
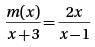
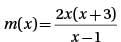
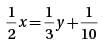
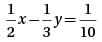
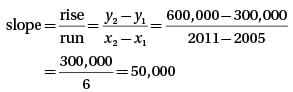
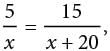 what is the value of x/5?
what is the value of x/5?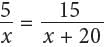 by x(x + 20) gives 15x = 5(x + 20). Distributing the 5 over the values within the parentheses yields 15x = 5x + 100, and then subtracting 5x from each side gives 10x = 100. Finally, dividing both sides by 10 gives x = 10. Therefore, the value of x/5 is 10/5 = 2.
by x(x + 20) gives 15x = 5(x + 20). Distributing the 5 over the values within the parentheses yields 15x = 5x + 100, and then subtracting 5x from each side gives 10x = 100. Finally, dividing both sides by 10 gives x = 10. Therefore, the value of x/5 is 10/5 = 2.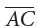 is the hypotenuse of right triangle ABC, and
is the hypotenuse of right triangle ABC, and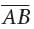 and
and 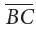 are the legs of right triangle ABC. By the Pythagorean theorem,
are the legs of right triangle ABC. By the Pythagorean theorem, 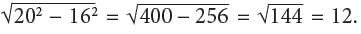 Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of angle F equals the measure of angle C. Thus, sinF = sinC. From the side lengths of triangle ABC, sinC = opposite side/hypotenuse = AB/AC = 12/20 = 3/5 . Therefore, sinF = 3/5. Either 3/5 or its decimal equivalent, .6, may be gridded as the correct answer.
Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of angle F equals the measure of angle C. Thus, sinF = sinC. From the side lengths of triangle ABC, sinC = opposite side/hypotenuse = AB/AC = 12/20 = 3/5 . Therefore, sinF = 3/5. Either 3/5 or its decimal equivalent, .6, may be gridded as the correct answer.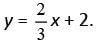 So the slope of the graph of the given equation is 2/3. In the xy-plane, when two nonvertical lines are perpendicular, the product of their slopes is −1. So, if m is the slope of a line perpendicular to the line with equation
So the slope of the graph of the given equation is 2/3. In the xy-plane, when two nonvertical lines are perpendicular, the product of their slopes is −1. So, if m is the slope of a line perpendicular to the line with equation  which yields m =
which yields m = 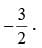 Of the given choices, only the equation in choice A can be rewritten in the form
Of the given choices, only the equation in choice A can be rewritten in the form 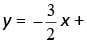 b , for some constant b. Therefore, the graph of the equation in choice A is perpendicular to the graph of the given equation.
b , for some constant b. Therefore, the graph of the equation in choice A is perpendicular to the graph of the given equation.