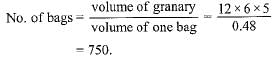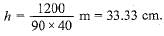Maths Mock Test- 3 - Class 10 MCQ
30 Questions MCQ Test - Maths Mock Test- 3
If two positive integers p and q are written as p=a2b2 and q=a3b, a,b are prime numbers then the vaue of L.C.M.(p,q)×H.C.F.(p,q) will be equal to
D, E, F are the mid points of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
If in the triangles ABC and DEF, angle A is equal to angle E, both are equal to 40°, AB : ED = AC : EF and angle F is 65°, then angle B is :-
In a right angled ΔABC, right angled at A, if AD ⊥ BC such that AD = p, If BC = a, CA = b and AB = c, then:
Out of the following options, the two angles that are together classified as complementary angles are
The number of terms common to the two A.P. s 2 + 5 + 8 + 11 + ...+ 98 and 3 + 8 + 13 + 18 +...+198
(p + q)th and (p – q)th terms of an A.P. are respectively m and n. The pth term is :
The diameter of a cycle wheel is 28 cm. The number of revolutions it makes in moving 13.2 km is
How many bags of grain can be stored in a cuboid granary 12 m x 6 m x 5 m. If each bag occupies a space of 0.48 m3 ?
In a swimming pool measuring 90 m x 40 m, 150 men take a dip. If the average displacement of water by a man is 8 m3, then rise in water level is
Direction: In the Following Questions, A Statement of Assertion (A) Is Followed by A Statement of Reason (R). Mark The Correct Choice As:
Assertion: If A and B are two independent events and it is given that P (A) = 2/5, P(B) = 3/5, then P (A ∩ B) = 6/25.
Reason : P (A ∩ B) = P (A) • P(B), where A and B are two independent events.
In ΔABC, AB = 5 cm, AC = 7 cm. If AD is the angle bisector of ∠A. Then BD : CD is:
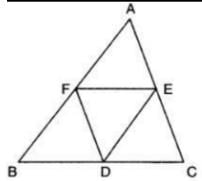
In a ΔABC, D is the mid-point of BC and E is mid-point of AD, BF passes through E. What is the ratio of AF : FC?
The vertices of the triangle formed by the lines x – y + 1 = 0, 3x + 2y – 12 = 0 and the x – axis are
If x = α and y = β is the solution of the equations x – y = 2 and x + y = 4, then
If the sum of n terms of an AP is 2n2 + 5n, then its nth term is –
If the last term of an AP is 119 and the 8th term from the end is 91 then the common difference of the AP is –
A circle drawn with origin (0,0) as the centre passes through the point 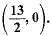 The point which does not lie in the interior of the circle is
The point which does not lie in the interior of the circle is


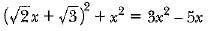

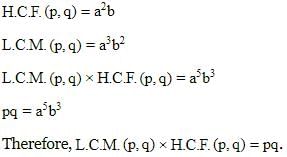


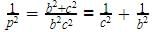
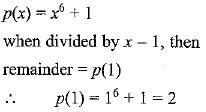
 is -
is -