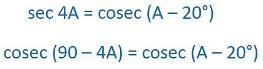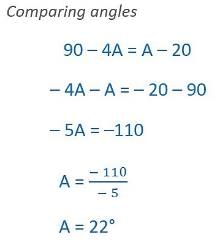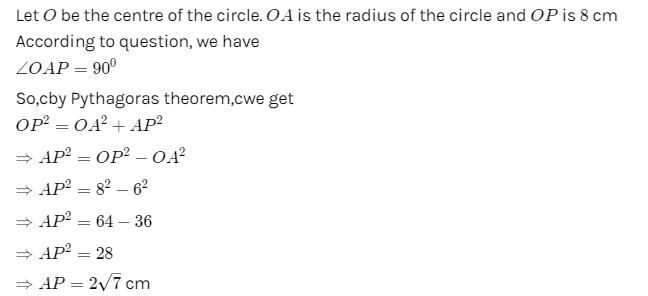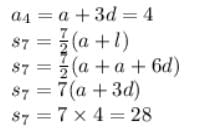Maths Mock Test- 4 - Class 10 MCQ
30 Questions MCQ Test - Maths Mock Test- 4
If sec 4A = cosec (A-20°),where 4A is an acute angle, find the value of A
Given that one of the zeroes of the cubic polynomial ax3 + bx2 + cx + d is zero, the product of the other two zeros is
Two parallel lines touch the circle at points A and B respectively, If area of the circle is 25πcm2, then AB is equal to
A line through point of contact and passing through centre of circle is known as
The length of the taragent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is
The diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 40 cm and 9 cm is:
The area of a circle with diameter 6 m exceeds the combined areas of circles with diameters 4m and 2 m by
The area of a circular plot is 9856 sq. m. The cost of fencing the plot at the rate of Rs. 6 per meter will be
In ΔABC and ΔDEF, ∠A = 50°, ∠B = 70°, ∠C = 60°, ∠D = 60°, ∠E = 70°, ∠F = 50°, then ΔABC is similar to:
The angle of elevation from a point 30 metre from the base of tree as level ground to the top of the tree is 60°. The height of the tree is :
Two natural numbers whose sum is 85 and the least common multiple is 102 are:
The fourth term of an A.P. is 4. Then the sum of the first 7 terms is :
If {an} = {2.5, 2.51, 2.52,...} and {bn} = {3.72, 3.73, 3.74,...} be two AP's, then a100005 – b100005 =
Given that one of the zeroes of the cubic polynomial ax3 + bx2 + cx + d is zero, the product of the other two zeroes is
Given that two of the zeros of the cubic polynomial ax3 + bx2 + cx + d are 0, the value of c is
In an equilateral triangle, the incentre, circumcentre, orthocentre and centroid are:
In the adjoining figure D is the midpoint of BC of a ΔABC. DM and DN are the perpendiculars on AB and AC respectively and DM = DN, then the ΔABC is :
If two positive integers a and b are written as a = x3y2 and b = xy3; x, y are prime numbers, then HCF (a, b) is
The sum of the diameters of two circles is 280 cm and the difference of their circumferences is 88 cm. Then the larger of the two radii is
If the perimeter and area of a circle are numerically equal, then the radius of the circle is
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then
The volume of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
A system of two linear equations in two variables is consistent, if their graphs