Matrix MCQ - 3 - Mathematics MCQ
30 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Matrix MCQ - 3
A matrix A such that Am = 0 for some positive integer and Ak ≠ 0 for any k < m, is said to be
Let A and B two n × n matrices over real numbers. Let rank(M) and det(M) denote the rank and determinant of a matrix M, respectively. Consider the following statements.
I. rank(AB) = rank(A) rank(B)
II. det(AB) = det(A) det(B)
III. rank(A + B) ≤ rank(A) + rank(B)
IV. det(A + B) ≤ det(A) + det(B)
Which of the above statements are TRUE?
If A and B are two odd order Skew — symmetric matrices such that AB = BA, then what is the matrix AB?
To convert a Hermitian Matrix into Skew Hermitian Matrix, the Hermitian Matrix must be multiplied by
Which is not correct? If A is any square matrix, then... is Hermitian Matrix
If A and B are symmetric matrices of the same order, then which one of the following is not correct?
If A =  satisfies the matrix equation A2 — kA + 2I = 0, then what is the value of k?
satisfies the matrix equation A2 — kA + 2I = 0, then what is the value of k?
Under which one of the following condition does the system of equations  have a unique solution?
have a unique solution?
One of the integrating factor of the differential equation
(y2 – 3xy)dx + (x2 – xy)dy = 0 is
The points ( x1, y1 ) , ( x2, y2), ( x3, y3) are collinear if the rank of the matrix 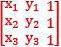 is
is
A neccessary condition for the linear equations a1x + b1 = 0 and a2x + b2 = 0, to have a common solution is that
A necesary and sufficient condition for the linear equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 to possess a unique solution is that
Let A and B be any two n x n matrices and tr(A) = 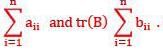 Consider the following statement
Consider the following statement
I. tr(AB) = tr(BA)
II. tr(A + B) = tr. (A) + tr(B)
Which of the following statement given above is/are correct?
|
27 docs|150 tests
|


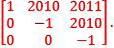 Then,
Then,




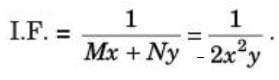

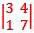 is
is











