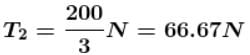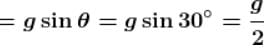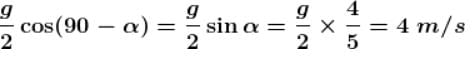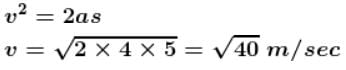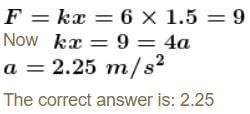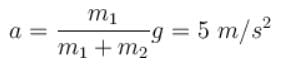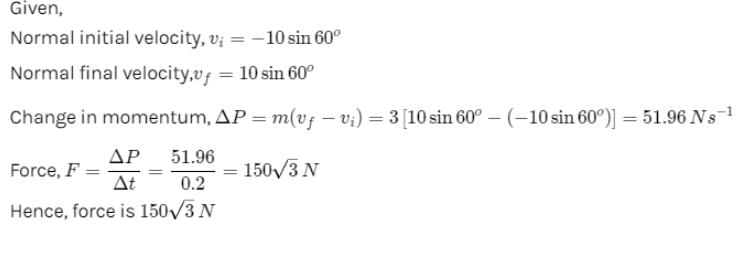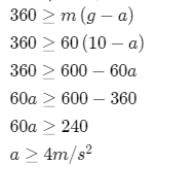Newton's Law Of Motion NAT Level - 1 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Newton's Law Of Motion NAT Level - 1
Figure shows two pulley arrangements for lifting a mass m. In (a) the mass is lifted by attaching a mass 2m. While in (b) the mass is filled by pulling the other end with a downward force F = 2mg. If fa and fb are the accelerations of the two masses such that 
Find the value of α
(Assume string is massless and pulley is ideal)
.
Find the value of α.
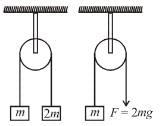
Figure shows a 5kg ladder hanging from a string that is connected with a ceiling and is having a spring balance connected in between. A boy of mass 25kg is climbing up the ladder at acceleration 1m/s2. Assuming the spring balance and the string to be massless and the spring to show a constant reading the reading to the spring balance ( in kg ) is........... Take g = 10m/s2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
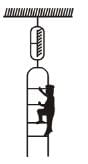
A man of mass m stands on a platform of equal mass m and pulls himself by two ropes passing over pulleys as shown. If he pulls each rope with a force half of his weight, his upward acceleration would be (in m/s2)
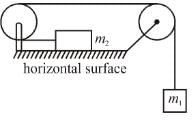
In the system shown in figure mA = 4m, mB = 3m and mC = 8m. Friction is absent everywhere. String is light and inextensible. If the system is released from rest find the acceleration ( in m/s–2) of block B. ( Take g = 10 m/s2)
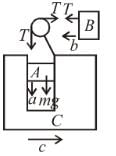
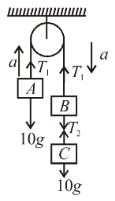
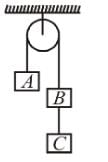
Three blocks A, B and C of mass 10kg each are hanging on a string passing over a fixed frictionless pulley as shown in figure. The tension (in Newton) in the string connecting blocks B and C is ......... Take g =10 m/s2
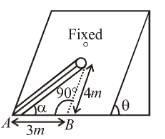
There is an inclined surface of inclination θ = 30º. A smooth groove is cut into it forming angle α with AB. A steel ball is free to slide along the groove. If the ball is released from the point O at top end of the groove, the speed when it when it comes to A in m/s is ........... Take g = 10 m/s2
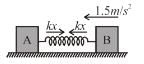
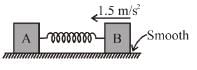
Two blocks A and B with mass 4kg and 6kg respectively are connected by a stretched spring of negligible mass as in figure. When the two block are released simultaneously the initial acceleration of B is 1.5m/s2 westward. The acceleration of A (in m/s2) is:
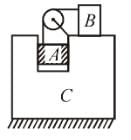
Consider the system as shown in the figure. The pulley and the string are light and all the surfaces are frictionless. The tension (in Newton) in the string is ............ ( g = 10m/s2 )
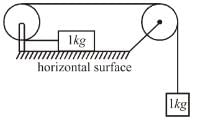
A body of mass 3kg hits a wall at an angle of 60° and with speed of 10m/s and returns at the same angle. The impact time is 0.2sec. Calculate force (in Newton) exerted on the wall :
One end of massless rope, which passes over a massless and frictionless pulley P is tied to a hook C while the other end is free. Maximum vertical force that the clamp can bear is 360N. With what value of minimum safe acceleration (in ms–2) can a man of 60kg climb down the rope?
Important Questions for Newton's Law Of Motion NAT Level - 1
Newton's Law Of Motion NAT Level - 1 MCQs with Answers
Online Tests for Newton's Law Of Motion NAT Level - 1 Topic wise Tests for IIT JAM Physics
|
© EduRev
|
Education Revolution
|
|
