Olympiad Test: Comparing Quantities - Class 8 MCQ
20 Questions MCQ Test - Olympiad Test: Comparing Quantities
A sum of money, at compound interest, yields Rs. 200 and Rs. 220 at the end of first and second years respectively. What is the rate percent?
The sale price of a shirt is Rs.176. If a discount of 20% is allowed on its marked price, what is the marked price of the shirt?
The difference in S.I. and C.I. on a certain sum of money in 2 years at 15% p.a. is Rs.144. Find the sum.
In what time will a sum of Rs. 800 at 5% p.a. C.I. amount to Rs. 882?
What is the C.I. on Rs. 8000 for 1 year at 5% p.a. payable half-yearly?
Raghu borrowed Rs. 25000 at 20% p.a. compounded half-yearly. What amount of money will clear his debt after 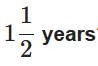 ?
?
In what time will Rs.1000 amount to Rs.1331 at 10% p.a. compounded annually?
The present population of a town is 25000. It grows at 4%, 5% and 8% during first year, second year and third year respectively. Find the population after 3 years.
The value of an article which was purchased 2 years ago, depreciates at 12% per annum. If its present value is Rs.9680, what is the price at which it was purchased?
The cost of a vehicle is Rs.175000. If its value depreciates at the rate of 20% per annum, find the total depreciation after 3 years.
The C.I. on a certain sum for 2 years is Rs. 410 and S.I. is Rs. 400. What is the rate of interest per annum?
The C.I. on a certain sum for 2 years at 10% per annum is Rs. 525. Calculate the S.I. on the same sum for double the time at half the rate percent per annum.
The S.I. on a sum of money for two years is Rs. 660, while C.I. is Rs.696.30, the rate of interest being the same in both the cases. Find the rate of interest.
A sum of money doubles itself in 3 years at C.I., when the interest is compounded annually. In how many years will it amount to 16 times of itself?
The C.I. on a certain sum at 5% for 2 years is Rs. 328. Calculate the S.I. for the sum at the same rate and for the same period.
Find the amount on Rs.12500 for 2 years compounded annually, the rate of interest being 15% for the first year and 16% for the second year.
Sugar is bought at Rs.16.20 per kg and sold at Rs.17.28 per kg. What is the gain percent?
A woman bought two packs of toffees, with the same of number of toffees in each pack. She bought the first pack at 25 paise per toffee and the second pack at 3 toffees for 65 paise. She mixed them together and sold at Rs.3.50 a dozen. What is her gain percent?
A man bought 542 kg of sugar for Rs. 7560.90and sold it so as to gain 20%. What is the selling price per kilogram of sugar?
A trader marks his goods 30% above the cost price but makes a reduction of 25/4 on the marked price for ready money. What is his gain percent?


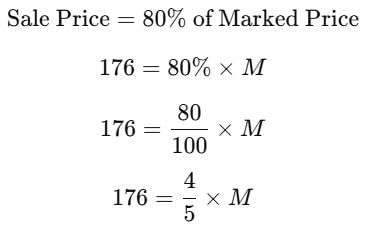
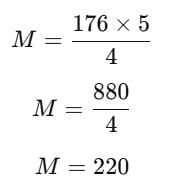

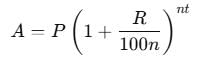
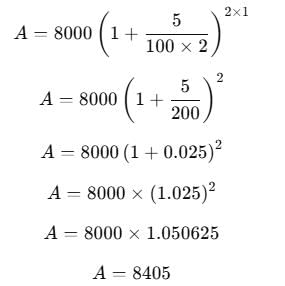
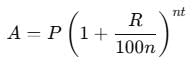
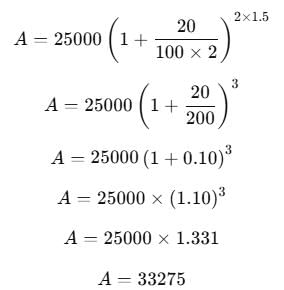
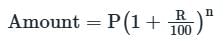
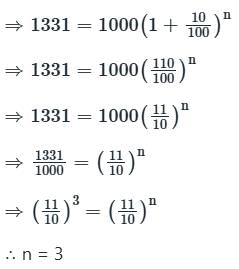
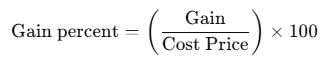
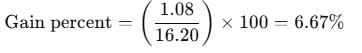
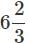 .
.










