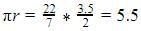Explore Exams
Login Signup
Sign in Open App
CTET & State TET Exam  >  CTET & State TET Test  >  Mathematics & Pedagogy Paper 2 for CTET & TET Exams  >  Olympiad Test: Mensuration - CTET & State TET MCQ

Olympiad Test: Mensuration - Free MCQ with solutions CTET Mathematics


MCQ Practice Test & Solutions: Olympiad Test: Mensuration (20 Questions)

You can prepare effectively for CTET & State TET Mathematics & Pedagogy Paper 2 for CTET & TET Exams with this dedicated MCQ Practice Test (available with solutions) on the important topic of "Olympiad Test: Mensuration". These 20 questions have been designed by the experts with the latest curriculum of CTET & State TET 2026, to help you master the concept.

Test Highlights:

  • - Format: Multiple Choice Questions (MCQ)
  • - Duration: 20 minutes
  • - Number of Questions: 20

Sign up on EduRev for free to attempt this test and track your preparation progress.

Olympiad Test: Mensuration - Question 1
Save

The parallel sides of a trapezium are 25 cm and 13 cm. Its non-parallel sides are equal, each being 10 cm. Find the area of the trapezium. 

Detailed Solution: Question 1

Area of trapezium= 1/2*d*(a+b) sq. Units.

Where d= perpendicular distance between parellel sides which are a & b respectively, 25 &13 cm.

25–13=12, 12/2= 6 cm is base of RT. Angled ∆.

Non parallel sides=10cm, this is hypotenuese of this ∆.

Find ‘d ‘ to solve.

d=√{102–62}=8 cm.

Area of trapezium= 1/2*8*(25+13)=152 cm2

Olympiad Test: Mensuration - Question 2
Save

Find the area of the given quadrilateral.

Detailed Solution: Question 2

Quad ABCD is made of two triangles ADC and ABC 

so, area(ABCD) = area(ABC) + area(ADC)

= 4 x 12/2 + 3.5 x12/2

= 24 + 21

= 45 cm2

Clear all your doubts with EduRev
Olympiad Test: Mensuration - Question 3
Save

Find the altitude of a trapezium, the sum of the lengths of whose bases is 6.5 cm and whose area is 26 cm2.

Detailed Solution: Question 3

Problem:
Find the altitude of a trapezium, the sum of the lengths of whose bases is 6.5 cm and whose area is 26 cm2.

To find the altitude of the trapezium, we can use the formula for the area of a trapezium:
Area = (1/2) * (sum of bases) * (altitude)
Given that the sum of the lengths of the bases is 6.5 cm and the area is 26 cm2, we can set up the equation:
26 = (1/2) * 6.5 * altitude
Simplifying the equation:
52 = 6.5 * altitude
Dividing both sides by 6.5:
altitude = 52 / 6.5
altitude = 8 cm
The altitude of the trapezium is 8 cm.
Answer: B. 8 cm

Olympiad Test: Mensuration - Question 4
Save

Find the total surface area of a cube whose volume is 343 cm3.

Detailed Solution: Question 4

volume=(side)^3
so, 343=(side)^3
cube root of 343=side
cube root of 343=7
side=7cm
Surface area=6(side)^2
Surface area=6 x 7^2
Surface area=6 x 49
Surface area=294 cm^2

Olympiad Test: Mensuration - Question 5
Save

A cylindrical tank has a capacity of 5632 m3. If the diameter of its base is 16 m, find its depth.

Detailed Solution: Question 5


Given:
- Capacity of the tank = 5632 m^3
- Diameter of the base = 16 m
We need to find the depth of the tank.
To find the depth, we can use the formula for the volume of a cylinder:
Volume = π * r^2 * h
where:
- π is a constant approximately equal to 3.14
- r is the radius of the base
- h is the height (or depth) of the cylinder
Step 1: Find the radius of the base:
The diameter of the base is given as 16 m. We can use the formula for the radius of a circle to find the radius:
Radius = Diameter / 2 = 16 / 2 = 8 m
Step 2: Substitute the values into the volume formula:
5632 = 3.14 * 8^2 * h
Simplifying the equation:
5632 = 3.14 * 64 * h
5632 = 200.96 * h
Step 3: Solve for h:
h = 5632 / 200.96
h ≈ 28 m
Therefore, the depth of the cylindrical tank is approximately 28 m.
Answer: D. 28 m

Olympiad Test: Mensuration - Question 6
Save

Find the area of a rhombus whose diagonals are of lengths 20 cm and 16 cm.

Detailed Solution: Question 6

Area of rhombus =1/2 ×d1×d2
Length of the one diagonal= 20 cm
Length of the other diagonal =16 cm
Area of the rhombus =1/2×20×16
= 1×10×16
= 160
The area of the rhombus is 160cm^2.

Olympiad Test: Mensuration - Question 7
Save

Find the area of the given figure.

Olympiad Test: Mensuration - Question 8
Save

Surface area of a cuboid = __________

Detailed Solution: Question 8

Total Surface Area of Cuboid: 2(lb + bh + hl)
L = length
B = Breadth
H = Height

Olympiad Test: Mensuration - Question 9
Save

Find the volume of a cuboid whose length is 8 cm, breadth 6 cm and height 3.5 cm. 

Detailed Solution: Question 9

Length of the cuboid = 8 cm

Breadth of the cuboid = 6 cm

Height of the cuboid = 3.5 cm

Volume of the cuboid = length × breadth × height

= 8 x 6 x 3.5 = 168cm3

Therefore,volume of  the cuboid = 168cm3

Olympiad Test: Mensuration - Question 10
Save

A godown is in the form of a cuboid of measures 60 m × 40 m × 30 m. How many cuboidal boxes can be stored in it if the volume of one box is 0.8 m3?

Detailed Solution: Question 10


Given:
Dimensions of the godown: 60 m × 40 m × 30 m
Volume of one box: 0.8 m³
To find:
Number of cuboidal boxes that can be stored in the godown
Formula:
Volume of a cuboid = length × width × height
Solution Steps:
1. Calculate the volume of the godown using the given dimensions:
Volume of godown = 60 m × 40 m × 30 m = 72000 m³
2. Divide the volume of the godown by the volume of one box to find the number of boxes that can be stored:
Number of boxes = Volume of godown / Volume of one box
Number of boxes = 72000 m³ / 0.8 m³ = 90000
Answer:
The number of cuboidal boxes that can be stored in the godown is 90000.
So, the correct answer is option D.

Olympiad Test: Mensuration - Question 11
Save

The perimeter of a trapezium is 52 cm. Its non-parallel sides are 10 cm each and the distance between two parallel sides is 8 cm. Find the area of the trapezium.

Detailed Solution: Question 11

Option A is correct.

Sum of the two non-parallel sides = 2 × 10 = 20 cm.

Sum of the two parallel sides = 52 - 20 = 32 cm.

Area of a trapezium = 1/2 × (sum of parallel sides) × height.

Area = 1/2 × 32 × 8

Area = 128 cm2. Hence option A is correct.

Olympiad Test: Mensuration - Question 12
Save

The cost of papering the wall of a room, 12 m long, at the rate of Rs. 1.35 per square meter is Rs. 340.20. The cost of matting the floor at Re. 0.85 per square metre is Rs. 91.80. Find the height of the room.

Detailed Solution: Question 12

Let the length of room = l = 12 m
breadth of room = b m
height of room = h m
Cost of matting the floor @ Re. 0.85 per m^2 = Rs. 91.80
floor area = 91.80 / 0.85 = 108 m^2
⇒ l * b = 108
⇒ 12 * b = 108
⇒ b = 108/12
⇒ b = 9 m
cost of papering wall @ Rs. 1.35 per m^2 = Rs. 340.20
wall area is the lateral surface area.
wall area = lateral surface area = 340.20 / 1.35 = 252 m^2
⇒ 2h(l+b) = 252
⇒ 2h(12+9) = 252
⇒ 2h*21 = 252
⇒ h = 252/(2*21) 
⇒ h = 6 m
Height of room is 6m.

Olympiad Test: Mensuration - Question 13
Save

The area of a trapezium is 384 cm2. Its parallel sides are in the ratio 3:5 and the distance between them is 12 cm. Find the length of each parallel side. 

Detailed Solution: Question 13


Given:
- Area of the trapezium = 384 cm^2
- Ratio of the parallel sides = 3:5
- Distance between the parallel sides = 12 cm
Let the lengths of the parallel sides be 3x and 5x, where x is a constant.
Step 1: Write the formula for the area of a trapezium:
Area = (sum of parallel sides) * (distance between them) / 2
Step 2: Substitute the given values into the formula:
384 = (3x + 5x) * 12 / 2
Step 3: Simplify the equation:
384 = 8x * 12 / 2
384 = 96x
Step 4: Solve for x:
x = 384 / 96
x = 4
Step 5: Find the lengths of the parallel sides:
3x = 3 * 4 = 12 cm
5x = 5 * 4 = 20 cm
Therefore, the lengths of the parallel sides are 12 cm and 20 cm.
Hence, the correct answer is option C: 12 cm and 20 cm.

Olympiad Test: Mensuration - Question 14
Save

In the given figure find the area of the path.

Detailed Solution: Question 14

Area of Rectangle ABCD = 110*150 = 16500cm2
Area of rectangle EFGH = (150-10)(110-10) = 14000cm2
Area of path = 16500-14000 = 2500cm2

Olympiad Test: Mensuration - Question 15
Save

The area of a rhombus is 28 cm2 and one of its diagonals is 4 cm. Find its perimeter.

Detailed Solution: Question 15


Given:
- The area of the rhombus is 28 cm^2.
- One of its diagonals is 4 cm.
To find:
- The perimeter of the rhombus.
Step 1: Find the length of the other diagonal.
- We know that the area of a rhombus can be calculated using the formula: Area = (d1 * d2) / 2, where d1 and d2 are the lengths of the diagonals.
- Since the area is given as 28 cm^2 and one diagonal is given as 4 cm, we can rearrange the formula to find the length of the other diagonal.
- 28 = (4 * d2) / 2
- 56 = 4 * d2
- d2 = 56 / 4
- d2 = 14 cm
Step 2: Find the side length of the rhombus.
- The side length of a rhombus can be found using the formula: s = √(Area / sinθ), where θ is the angle between the diagonals.
- Since the diagonals of a rhombus are perpendicular bisectors of each other, the angle between them is 90 degrees.
- sin90 = 1, so the formula simplifies to s = √Area.
- Therefore, the side length of the rhombus is √28 cm.
Step 3: Find the perimeter of the rhombus.
- The perimeter of a rhombus is simply 4 times the length of its sides.
- Therefore, the perimeter of the rhombus is 4 * √28 cm.
Step 4: Calculate the perimeter.
- Substituting the value of √28, we get the perimeter as 4 * √28 cm.
- Simplifying further, the perimeter is equal to 4 * 2√7 cm.
- This gives us a final answer of 8√7 cm.
Therefore, the correct answer is A: 8√7 cm.

Olympiad Test: Mensuration - Question 16
Save

Find the side of a cube whose surface area is 2400 cm2.

Detailed Solution: Question 16

Option B is correct.

Use the formula surface area = 6 × (side)2 for a cube.

Substitute the given surface area: 2400 cm2 = 6 × (side)2.

Divide both sides by 6 to get (side)2 = 400.

Take the square root of both sides: side = √400 = 20 cm.

Therefore the side of the cube is 20 cm, which matches option B.

Olympiad Test: Mensuration - Question 17
Save

Find the height of a cuboid whose volume is 275 cm3 and base area is 25 cm2

Detailed Solution: Question 17

Area of the base = Product of length and breadth

Volume of cuboid = Length x breadth x Height
= Area of its base x Height
275 = 25 x Height
Height = 275 / 25 cm
=11 cm

Olympiad Test: Mensuration - Question 18
Save

Find the height of cuboid whose volume is 490 cm3 and base area is 35 cm2. 

Detailed Solution: Question 18

Volume of cuboid = base area × height
490 = 35 × height
height = 14cm.

Olympiad Test: Mensuration - Question 19
Save

Surface area of a cube = _________

Detailed Solution: Question 19


To find the surface area of a cube, we need to calculate the area of each face and then sum them up.
Step 1: Identify the formula for the surface area of a cube:
The formula for the surface area of a cube is given by 6 times the square of the length of one side (s):
Surface Area = 6s^2
Step 2: Break down the formula and calculate:
- Each face of a cube has the same length, so we can substitute s for l in the formula.
- Calculate the square of the length:
l^2
- Multiply the square of the length by 6:
6 * l^2
Step 3: Write the final answer:
The surface area of a cube is 6l^2.
Answer: A: 6 l^2
Note: The surface area of a cube is always equal to 6 times the square of one side length.

Olympiad Test: Mensuration - Question 20
Save

Detailed Solution: Question 20

Circumference of semi circle = 
perimeter = sum of two sides + circumference = 4 + 5.5 = 9.5cm

83 videos|266 docs|69 tests
Join Course
Information about Olympiad Test: Mensuration Page
In this test you can find the Exam questions for Olympiad Test: Mensuration solved & explained in the simplest way possible. Besides giving Questions and answers for Olympiad Test: Mensuration, EduRev gives you an ample number of Online tests for practice
Download as PDF

About this CTET & State TET Practice Test

This test contains 20 MCQs on Olympiad Test: Mensuration with detailed solutions for each question. It is part of the Mathematics & Pedagogy Paper 2 for CTET & TET Exams course on EduRev, designed to align with the current CTET & State TET syllabus. Each solution explains not just the correct answer but also gives you an understanding of the topic — not just to attempt the question but also help you prepare for the exam with practice.

Explore more CTET & State TET Study Resources

If you found this Olympiad Test: Mensuration MCQ Test helpful, you can further enhance your CTET & State TET preparation with in-depth courses on EduRev, for all the subjects and topics available in Mathematics & Pedagogy Paper 2 for CTET & TET Exams course. The course offers:
  • Video Lectures: covering all the topics of Mathematics & Pedagogy Paper 2 for CTET & TET Exams
  • Notes for Revision: offering revision notes, important questions, summaries, flashcards, cheatsheets & more for CTET & State TET preparation
  • MCQ Test: variety of questions as per the pattern of CTET & State TET exam
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup