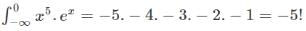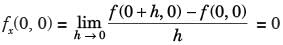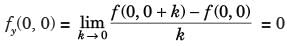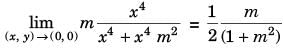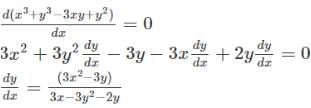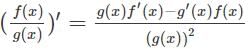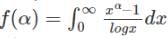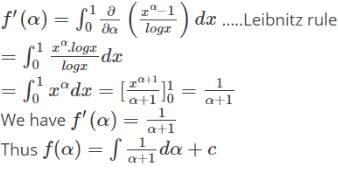Partial Differential Equation MCQ - 2 - IIT JAM MCQ
15 Questions MCQ Test - Partial Differential Equation MCQ - 2
General solution of pde given below is (y2+ z2+ x2 )p - 2xyq + 2xz = 0
If z = 3xy + 4x2, what is the value of ∂z / ∂x?
The general integral of z(xp — yq) = y2 — x2 is
What is the reason behind the non-existence of any real function which satisfies the differential equation, (y’)2 + 1 = 0?
What are the tangents to the curve x3 + y3 = 3axy at the origin?
Let f : R2 → R be defined by
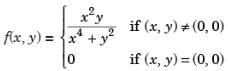
Which of the following statements holds regarding the continuity and the existence of partial derivatives of f at (0, 0)?
Find the order of the difference equation Δ3yn – Δ2yn – Δyn = 3
Find the differentiation of x3 + y3 – 3xy + y2 = 0?
Which of the following relations hold true for division rule of differentiation?
The integral surface of the p. d. e 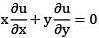 satisfying the condition u ( 1 , y ) = y is given by
satisfying the condition u ( 1 , y ) = y is given by
When solved by the method of Differentiation for the given integral i.e 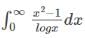 the result obtained is given by _______.
the result obtained is given by _______.


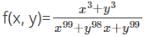
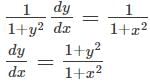

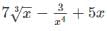 with respect x?
with respect x?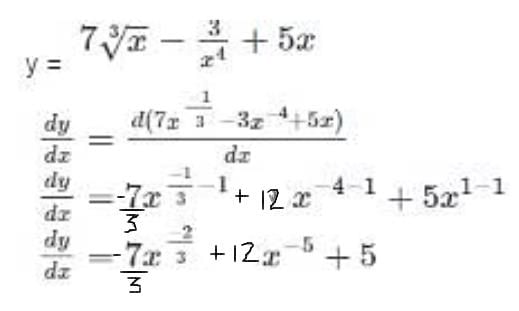
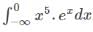
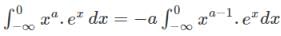 We have
We have