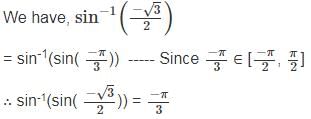RPSC Senior Grade II (Mathematics) Mock Test - 2 - REET MCQ
30 Questions MCQ Test - RPSC Senior Grade II (Mathematics) Mock Test - 2
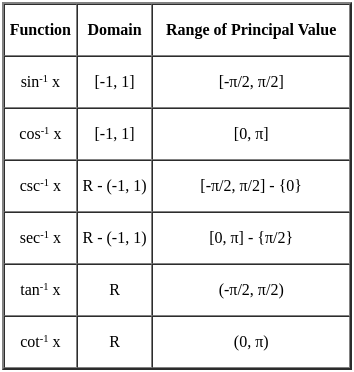
Which of the following statements is not true for the objectives of mathematics education when compared with its aims?
Which of the following need NOT be an aspect of unit planning in mathematics?
In which method the proof of a geometric theorem proceeds just the reverse way of the proof given in the textbooks?
I. Analytic method
II. Synthetic method
I. Analytic method
II. Synthetic method
Which of the following is/are the tools and techniques of assessment for learning mathematics?
I. Written, oral and performance tests and tasks
II. Projects and Work
III. Child's participation in doing mathematical work
The generator of the group G = {a, a2, a3, a4, a5, a6 = e} is
Find the equation of the directrix of the parabola x2 = - 8y ?
A glass jar contains 6 black, 8 blue, 4 white and 3 red marbles. If a single marble is chosen at random from the jar, what is the probability that it is blue or red?
Two unbiased dices are thrown what is the probability of getting a sum of 10?
Find the area of a rhombus whose diagonals are of lengths 10 cm and 8.2 cm.
What are the order and degree respectively of the differential equation
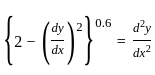 ?
?
Solve the following: 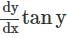 = sin(x + y) + sin(x − y)
= sin(x + y) + sin(x − y)
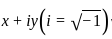 , when
, when
For the operator T on R3 defined by T(x, y, z) = (x - y, 2x + 3y + 2z, x + y + 2z), all eigenvalues and a basis for each eigenspace as
If the eigenvalues of the matrix 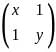 are in the ratio 3 ∶ 1 when y = 2, then x = ?
are in the ratio 3 ∶ 1 when y = 2, then x = ?
Every element of a group G when expressed as internal Direct product of a, b, c, ... z if and only of every element is uniquely expressed as ?
What is the rank of a 2 × 2 check board matrix?
If f is a continuous function from X to Y, then this property is called?
Find f(2) using newton divided difference formula for the data f(0) = 1, f(1) = 3, f(3) = 55.
The differential equation of the family of curves y2 = 4a(x + a) is :
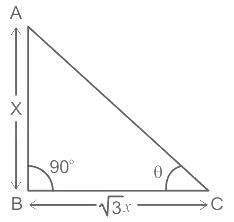
If the length of a shadow cast by a pole is √3 times the length of the pole, then the angle of elevation of the sun is -
The following sentences are steps involved in finding the H.C.F. of 29 and 24 by using Euclid's division algorithm. Arrange in sequential order from first to last.
(a) 5 = 1 × 5 + 0
(b) 29 = 24 × 1 + 5
(c) 24 = 5 × 4 + 1
If A = 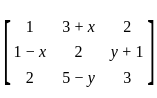 is a symmetric matrix, then 3x + y is equal to?
is a symmetric matrix, then 3x + y is equal to?
Find the distance between the directrices of the ellipse 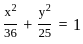 .
.
How many terms are there in G.P 4, 20, 100, … , 62500?
The length of the longest rod that can be placed in a cubical room is 40√3 cm. What is the volume of the cube?
A class has 175 students. The number of students studying one or more of the subjects in this class is as below :
Mathematics 100, Physics 70, Chemistry 46, Mathematics and Physics 30, Mathematics and Chemistry 28, Physics and Chemistry 28, Mathematics, Physics and Chemistry 18.
The number of students enrolled in Mathematics alone is :




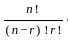
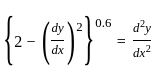
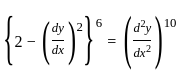
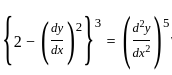
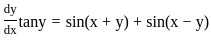
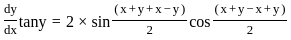
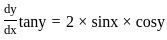
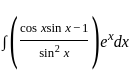 ?
?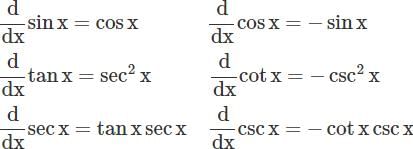

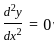 , then
, then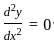
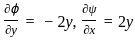
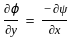
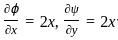
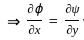
 = A (Say)
= A (Say)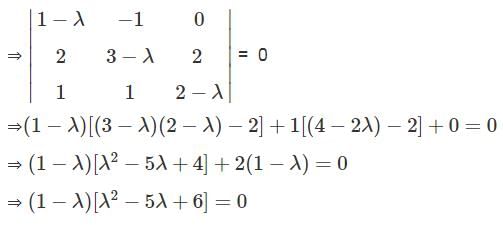
 be an eigen vector.
be an eigen vector.
 and
and 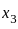 are dependent on each other.
are dependent on each other.

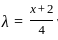 ............(i)
............(i)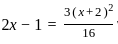
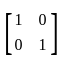

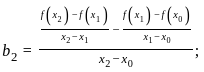
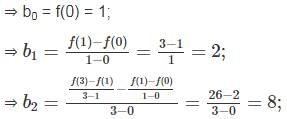
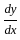 = 4a
= 4a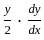
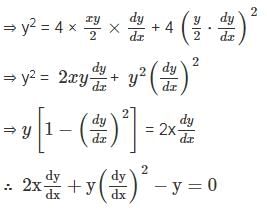
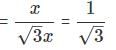
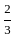 πr3
πr3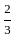 π (4.2)3 = 155.736 π
π (4.2)3 = 155.736 π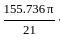 = 7.415 π ≈ 23.275
= 7.415 π ≈ 23.275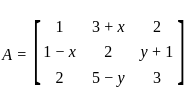
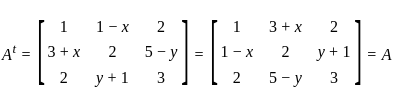
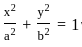 , a > b, is equal to
, a > b, is equal to 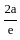 .
. .
.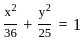 with the standard form, we get:
with the standard form, we get: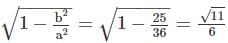 .
.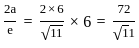 .
.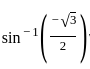 is
is