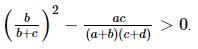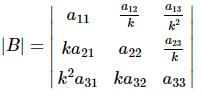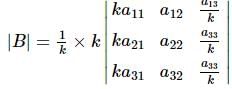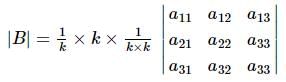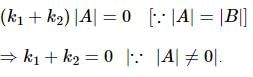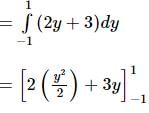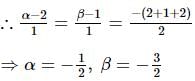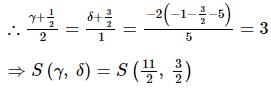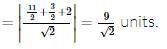SRMJEE Mock Test - 1 (Engineering) - JEE MCQ
30 Questions MCQ Test - SRMJEE Mock Test - 1 (Engineering)
In the figure shown below, the galvanometer shows no deflection. What is the value of resistance X?


Two water droplets coalesce to form a large drop. In this process,
A long-playing record revolves at a speed of 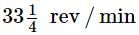 and has a radius of 15 cm. Two coins are placed at distances of 4 cm and 14 cm from the center of the record. If the coefficient of friction between the coin and the record is 0.15, choose the correct option:
and has a radius of 15 cm. Two coins are placed at distances of 4 cm and 14 cm from the center of the record. If the coefficient of friction between the coin and the record is 0.15, choose the correct option:
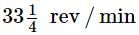 and has a radius of 15 cm. Two coins are placed at distances of 4 cm and 14 cm from the center of the record. If the coefficient of friction between the coin and the record is 0.15, choose the correct option:
and has a radius of 15 cm. Two coins are placed at distances of 4 cm and 14 cm from the center of the record. If the coefficient of friction between the coin and the record is 0.15, choose the correct option:The electrons of Rutherford's model would be expected to lose energy because, they
A square frame of side l carries a current and produces a magnetic field B at its center. The same current is passed through a circular loop having the same perimeter as the square. The field at its center is B'. The ratio of B/B' is:
Directions: In the following question, two statements are given. One is assertion and the other is reason. Examine the statements carefully and mark the correct answer according to the instructions given below.
Assertion: Copper reacts with dilute HCI to liberate hydrogen.
Reason: Hydrogen is present below Cu in the reactivity series.
The relative lowering of the vapour pressure of an aqueous solution containing a non-volatile solute is 0.0125. What is the molality of the solution?
The halogen compound which will not react with phenol to give ethers is
The half-life of the reaction did not change when the concentration of B alone was doubled. The rate increased by two times when the concentration of A alone was doubled. What is the unit of the rate constant for the above reaction?
In a triangle ABC, a = 4, b = 3 and A = 60°, then c is a root of the equation:
The line y = mx + c touches the ellipse = 1 if
If a, b, c, d are four consecutive coefficients in the binomial expansion of (1 + x)n, then the value of the expression 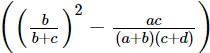 (where x > 0 and n ∈ N) is
(where x > 0 and n ∈ N) is
Let |A| = |aᵢⱼ|₃×₃ ≠ 0. Each element aᵢⱼ is multiplied by k⁽ⁱ⁻ʲ⁾. Let |B| be the resulting determinant. Given that k₁|A| + k₂|B| = 0, then k₁ + k₂ = ?
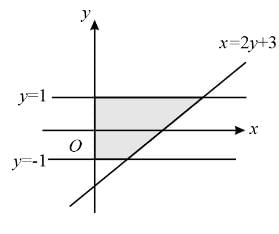
The area of the region bounded by the curve x = 2y + 3, the y-axis, and the lines y = 1 and y = -1 is:
A parabola with directrix x + y + 2 = 0 touches a line 2x + y - 5 = 0 at the point (2, 1). Then the semi-latus rectum of the parabola is:
The joint equation of a pair of straight lines, both of which pass through the origin and are perpendicular to the lines represented by the equation: y² + 3xy − 6x + 5y − 14 = 0 will be:
If ∫f(x) dx = g(x) and f⁻¹(x) is differentiable, then ∫f⁻¹(x) dx is equal to:
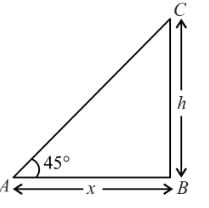
A person standing on the bank of a river finds that the angle of elevation of the top of a tower on the opposite bank is 45°. Then which of the following statements is correct.
The sum of three consecutive odd numbers is 1383. What is the largest number?
For real x, the function (x − a)(x − c) / (x − b) will assume all real values provided that:
The C.P. (Cost Price) of 10 articles is equal to the S.P. (Selling Price) of 15 articles. What is the profit or loss percentage?
From the word 'POSTSCRIPT,' how many independent words can be made without changing the order of the letters and using each letter only once?
What is the author's opinion about the competition for customers among micro-financiers?



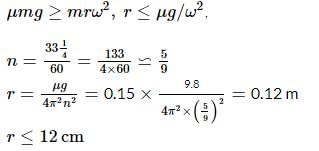
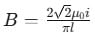
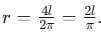 Magnetic field at the center:
Magnetic field at the center: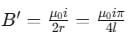
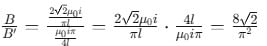
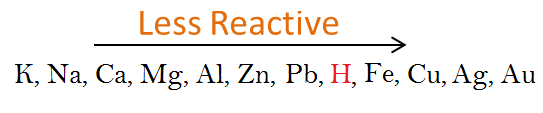
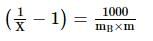
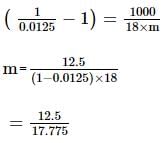
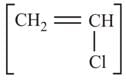
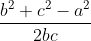
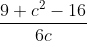

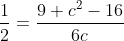

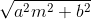
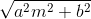 for all real m.
for all real m.