SRMJEE Mock Test - 6 (Engineering) - JEE MCQ
30 Questions MCQ Test - SRMJEE Mock Test - 6 (Engineering)
A body of mass m is placed on the earth's surface. It is taken from the earth's surface to a height h = 3R. What is the change in gravitational PE of the body?
If energy (E), velocity (V) and force (F) are taken as fundamental quantities, then what is the dimensional formula of mass?
A nucleus of mass 218 amu in free state decays to emit an α-particle. Kinetic energy of the α-particle emitted is 6.7 MeV. The recoil energy (in MeV) of the daughter nucleus is
A photocell employs photoelectric effect to convert
A point source S emitting light of wavelength 600 nm is placed at a very small height h above a flat reflecting surface AB (see figure). The intensity of the reflected light is 36% of the incident intensity. Interference fringes are observed on a screen placed parallel to the reflecting surface at a very large distance D from it.
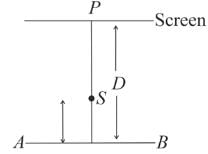
What is the shape of the interference fringes on the screen?
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x, respectively are T2 and T1 (T2>T1). The rate of heat transfer through the slab, in a steady state is 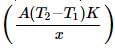 f, with f equals to
f, with f equals to
What is the resistance that must be connected in series with an inductance of 0.2 H such that the phase difference between current and emf is 45° when the frequency is 50 Hz?
Directions: In the following question, two statements are given. One is Assertion and the other is Reason. Examine the statements carefully and mark the correct answer according to the instructions given below.
Assertion: CO and CN are referred to as π acid ligands.
Reason: In CO and CN, vacant π type orbitals are present.
The emf of the cell Mg(s) | Mg²⁺ (0.01 M) || Sn²⁺ (0.1 M) | Sn(s) at 298 K is given.
Given:
- E°(Mg²⁺/Mg) = −2.34 V
- E°(Sn²⁺/Sn) = −0.14 V
Which of the following pairs of ions, when mixed in dilute solutions, may give a precipitate?
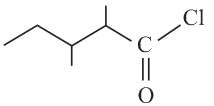
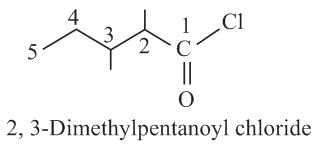
What will be the IUPAC name of this following compound?
Which intermediate is formed in the Reimer - Tiemann reaction?
 ,
,  ,
,  are mutually perpendicular vectors of equal magnitude, then the angle between (
are mutually perpendicular vectors of equal magnitude, then the angle between ( +
+  +
+  ) and
) and  is
is
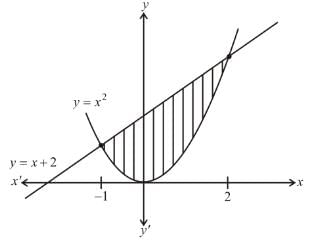
The area (in square units) of the region A = {(x, y) : x² ≤ y ≤ x + 2} is:
Let 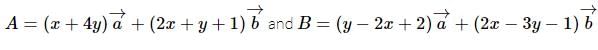 where
where 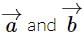 are non-collinear vectors, if 3A = 2B then
are non-collinear vectors, if 3A = 2B then
The locus of a perpendicular from the center upon the normal to the hyperbola 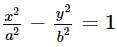 is
is
If α and β are the roots of the equation 2x² - 3x - 6 = 0, then the value of (α - β)² can be:
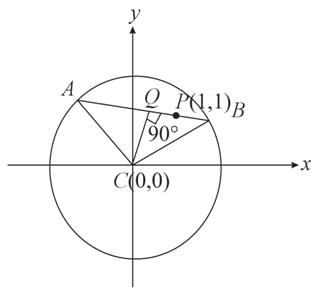
AB is a chord of x² + y² = 4, and P(1,1) trisects AB. Then, the length of the chord AB is:
Let A (0, 2), B (0, 2), and C be points on the parabola y² = x + 4 such that ∠CBA = π/2. Then the range of the ordinate of C is:
In the given figure, BD = DC and AB = AC. Find the measure of ∠ABE.

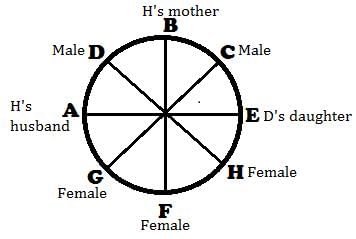
Study the following information carefully and answer the given question:
A, B, C, D, E, F, G and H are sitting around a circle facing the centre but not necessarily in the same order.
- B sits second to left of H's husband. No female is an immediate neighbour of B.
- D's daughter sits second to right of F. F is the sister of G. F is not an immediate neighbour of H's husband.
- Only one person sits between A and F. A is the father of G. H's brother D sits to the immediate right of H's mother. Only one person sits between H's mother and E.
- Only one person sits between H and G. G is the mother of C. G is not an immediate neighbour of E.
Which of the following is true with respect to the given seating arrangement?
The polynomial (ax² + bx + c)(ax² − dx − c), where ac ≠ 0, has:
Which of the following is the same in meaning as "deferred" written in underline in the passage?
Which of the following is opposite in meaning to "ramp up" written in underline in the passage?



 =
=  =
= 
 Change in gravitational PE = u2 – u1
Change in gravitational PE = u2 – u1 

 =
= 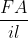
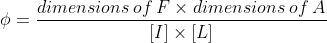

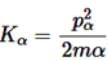

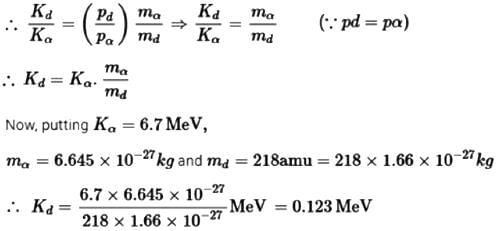
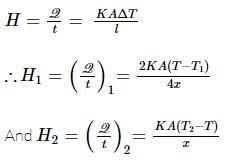
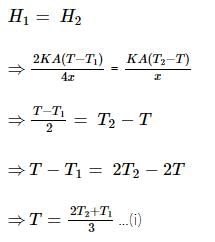
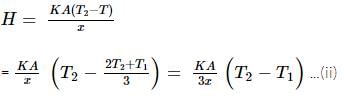
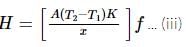
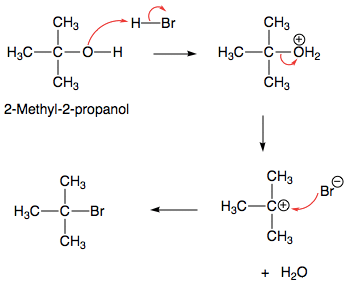
 R— CI + H2O
R— CI + H2O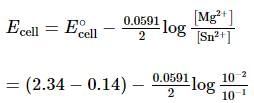
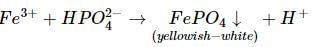
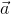 .
. 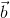 =
= 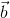 .
. 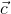 =
=  .
. 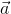 = 0
= 0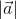 =
= 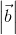 =
= 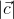 = a
= a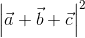 = a2 + b2 + c2 + 2 (
= a2 + b2 + c2 + 2 ( .
.  +
+  .
.  +
+  .
.  )
)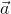 +
+ 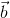 +
+ 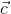 ) .
) . 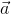 =
= 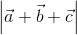
 cosθ
cosθ a2 +
a2 + 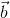 .
.  +
+ 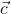 .
. 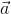 =
= a2 cos θ
a2 cos θ a2 =
a2 = a2 cosθ
a2 cosθ cosθ =
cosθ = 
 θ = cos-1
θ = cos-1


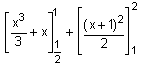

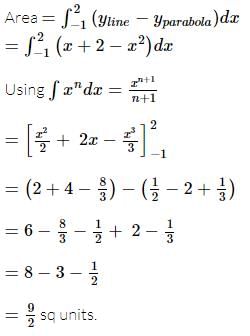
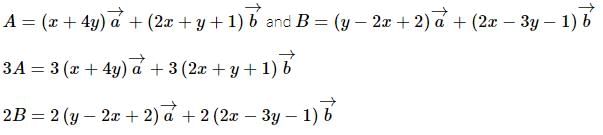
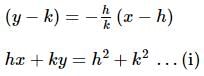
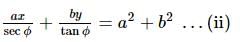
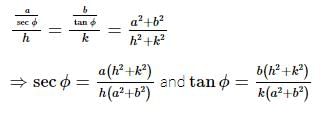
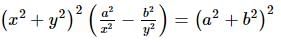
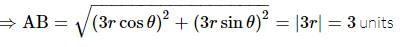
 = 64°
= 64°