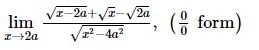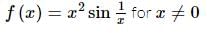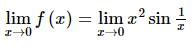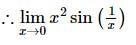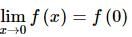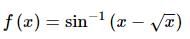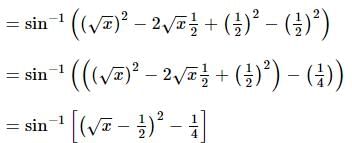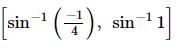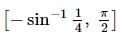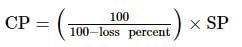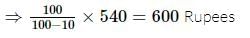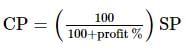SRMJEE Mock Test - 7 (Engineering) - JEE MCQ
30 Questions MCQ Test - SRMJEE Mock Test - 7 (Engineering)
Which of the following show(s) the particle and wave nature of electromagnetic waves and electrons?
The photoelectric effect is based upon the conservation of
The work function of lithium and copper are respectively 2.3 eV and 4.0 eV. Which one of the metals will be useful for the photoelectric cell working with visible light? (h = 6.6 × 10⁻³⁴ J·s, c = 3 × 10⁸ m/s)
An equilateral prism deviates a ray through 45° for two angles of incidence differing by 20°. The angles of incidence are:
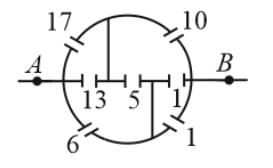
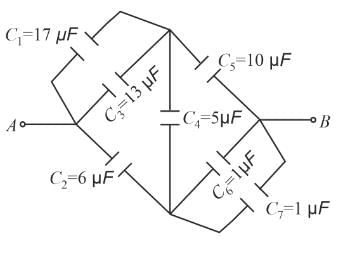
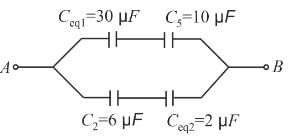
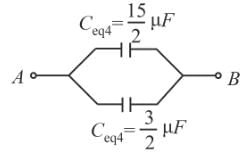
The equivalent capacitance across A and B (all capacitance are in μF) is
If x, v, and a denote the displacement, velocity, and acceleration of a particle executing simple harmonic motion with time period T, then which of the following does not change with time?
A gas under constant pressure of 4.5 × 10⁵ Pa, when subjected to 800 kJ of heat, changes the volume from 0.5 m³ to 2.0 m³. The change in internal energy of the gas is:
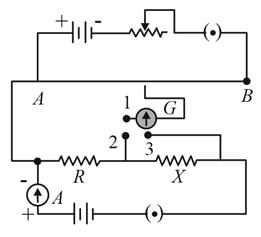
A potentiometer circuit is set up as shown. The potential gradient across the potentiometer wire, is k volt/cm and the ammeter, present in the circuit, reads 1.0 A when two way key is switched off. The balance points, when the key between the terminals (i) 1 and 2 (ii) 1 and 3, is plugged in, are found to be at lengths l1 cm and l2 cm respectively. The magnitudes, of the resistors R and X, in ohms, are then, equal, respectively, to
Thermal decomposition of N2O5 occurs as per the equation below:
2N2O5 → 4NO2 + O2
The correct statement is
Which of the following has the strongest base?

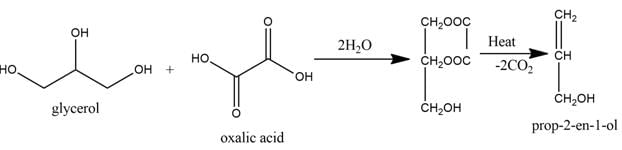
At 530 K, glycerol reacts with oxalic acid to produce
Among the following, in which species does the (n-1)dx²−y² orbital take part in hybridization?
If one root of the equation x2 + px + q = 0 is double the other, then p2/q is equal to
A and B are two independent events. The probability that both A and B occur is 1/6 and the probability that neither of them occurs is 1/3. Then, the respective probabilities of the two events are
For two complex numbers z1 and z2, satisfying |z1| = 12 and |z2 – 3 – 4i| = 5, the minimum value of |z1 – z2| is
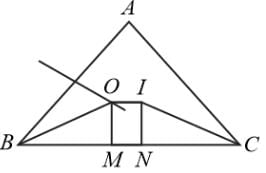
If in ΔABC the line joining the circumcentre and the incentre is parallel to BC, then
If f(x) = x² * sin(1/x), where x ≠ 0, then the value of the function f(x) at x = 0 is 0, so that the function is continuous at x = 0.
If x = ω - ω² - 2, where ω and ω² are the cube roots of unity, then the value of x⁴ + 3x³ + 2x² - 11x - 6 is:
The range of the function f(x) = sin⁻¹(x - √x) is:
The number of integral solutions of the inequality:
log₉(x + 1) + log₂(x + 1) - log₉(x + 1) - log₂(x + 1) + 1 < 0
is/are?
Directions: Read the following information and answer the question.
Five girls are sitting facing towards the North. Rekha is between Shalini and Neetu. Pooja is to the immediate right of Neetu, and Shalini is to the immediate right of Neha.
Who is sitting in the middle?
Rohan walks 3 km towards north and then turns left and walks 2 km. Then, he again turns left and walks 3 km. At that point, he turns left and walks 3 km. How far is he from the starting point?
Directions: Study the following information to answer the given question.
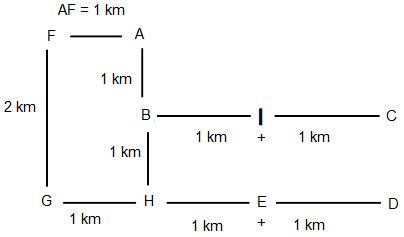
A, B, C, D, E, F, G, H and I are nine houses. C is 2 km to the east of B. A is 1 km to the north of B and H is 2 km to the south of A. G is 1 km to the west of H while D is 3 km to the east of G and F is 2 km to the north of G. I is situated just in the middle of B and C while E is just in the middle of H and D.
Distance between A and F is
A man sold a fan for 540 Rs losing 10% ( Loss of 10% ). At what price should he have sold it to gain 10%?



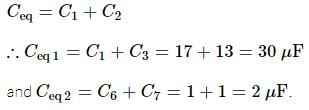
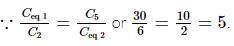
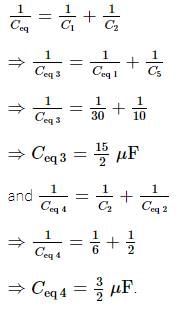
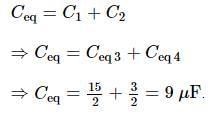
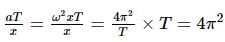
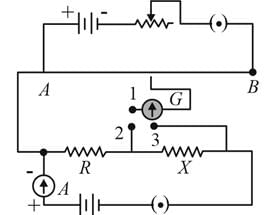
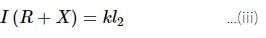
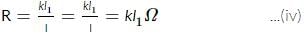
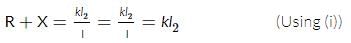
 (Using (iv))
(Using (iv))




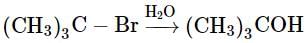 is
is is an example of substitution reaction
is an example of substitution reaction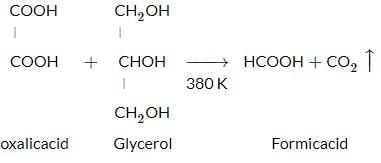
 + 3 .
+ 3 .  + ...
+ ...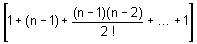
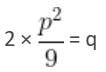
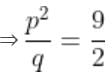

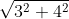 = 5
= 5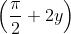
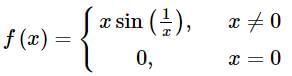 at x = 0 is
at x = 0 is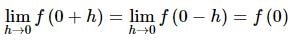
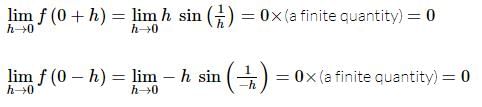
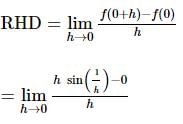
 is
is