Sequences And Series Of Real Numbers -6 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Sequences And Series Of Real Numbers -6
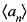 is bounded and bn —> 0, choose the appropriate conclusion from the following options
is bounded and bn —> 0, choose the appropriate conclusion from the following options
The value of x for which of the following series converges is
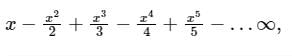
Suppose (cn) is a sequence of real numbers such that |cn|1/n exists and is non-zero. If the radius of convergence of the power series
cn xn is equal to r, then the radius of convergence of the power series
n2cnxn is
Let an = least power of 2 that divides n. For instance, a1 = 0, a2 = 1, a3 = 0, a4 = 2. Then, the sequence <an> is
If the sequence be defined by a1 = 1 and an+ 1 =
be defined by a1 = 1 and an+ 1 = 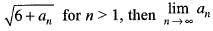 is equal to
is equal to
What is true for the sequence 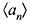 given by an
given by an 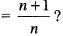
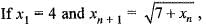 then the sequence {xn} converge to the positive root of the equation
then the sequence {xn} converge to the positive root of the equation
The sequence { xn } , where xn = 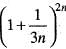 converge to
converge to
A sequence {an} may be defined by a recursion formula
|
27 docs|150 tests
|


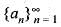 is decreasing and bounded, then
is decreasing and bounded, then 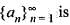
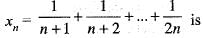

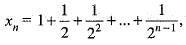
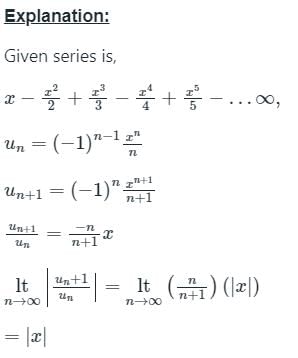

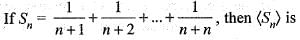



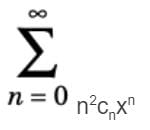 is
is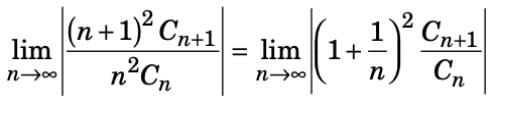
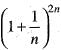 converge to
converge to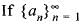 converges to a, for all n, a ≥ 0, then
converges to a, for all n, a ≥ 0, then 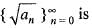
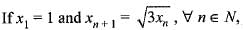 then the sequence {xn} converge to
then the sequence {xn} converge to converge to
converge to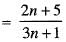 converges to
converges to











