Test: Area & Perimeter - 1 - CDS MCQ
15 Questions MCQ Test - Test: Area & Perimeter - 1
Anil grows tomatoes in his backyard which is in the shape of a square. Each tomato takes 1 cm2 in his backyard. This year, he has been able to grow 131 more tomatoes than last year. The shape of the backyard remained a square. How many tomatoes did Anil produce this year?
ABCD is a square drawn inside a square PTRS of sides 4 cm by joining midpoints of the sides PR, PT, TS, SR. Another square is drawn inside ABCD similarly. This process is repeated infinite number of times. Find the sum of all the squares.
PQRST is a pentagon in which all the interior angles are unequal. A circle of radius ‘r’ is inscribed in each of the vertices. Find the area of portion of circles falling inside the pentagon.
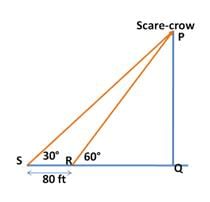
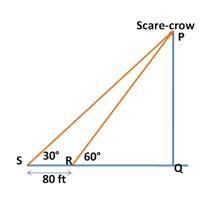
Raj stands in a corner of his square farm. Angle of elevation of a scarecrow placed in diagonally opposite corner is 60°. He starts walking backwards in a straight line and after 80ft he realizes that angle of elevation of the scarecrow now is 30°. What is area of the field?
The area of the circle is 2464 cm2 and the ratio of the breadth of the rectangle to radius of the circle is 6:7. If the circumference of the circle is equal to the perimeter of the rectangle, then what is the area of the rectangle.
A rectangular paper of width 7 cm is rolled along its width and a cylinder of radius 20 cm is formed. Find the volume of the cylinder.
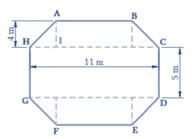
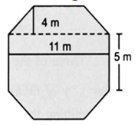
Top surface of a raised platform is in the shape of regular octagon as shown in the figure. Find the area of the octagonal surface.
The diagonal of a quadrilateral shaped field is 24 m and perpendicular dropped on it from the remaining opposite vertices are 6 m and 12 m. Find the area of the field.
A cube is inscribed in a hemisphere of radius R, such that four of its vertices lie on the base of the hemisphere and the other four touch the hemispherical surface of the half-sphere. What is the volume of the cube?
The maximum distance between two points of the unit cube is
The perimeter of a triangle is 28 cm and the inradius of the triangle is 2.5 cm. What is the area of the triangle?
An order was placed for the supply of a carpet whose breadth was 6 m and length was 1.44 times the breadth. What be the cost of a carpet whose length and breadth are 40% more and 25% more respectively than the first carpet. Given that the ratio of carpet is Rs. 45 per sq m?
All five faces of a regular pyramid with a square base are found to be of the same area. The height of the pyramid is 3 cm. The total area of all its surfaces (in cm2) is
A bicycle wheel makes 5000 revolutions in moving 11 km. What is the radius of the wheel?
The short and the long hands of a clock are 4 cm and 6 cm long respectively. What will be sum ofdistances travelled by their tips in 4 days? (Take p = 3.14)