Test: Automatic Control Systems - 2 - Electrical Engineering (EE) MCQ
25 Questions MCQ Test - Test: Automatic Control Systems - 2
Assertion (A): If points at infinity are included, G(s) has same number of poles and zeros.
Reason (R): The function 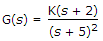 has a zero at s = - 2.
has a zero at s = - 2.
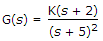 has a zero at s = - 2.
has a zero at s = - 2.If the characteristic equation is (λ + 1) (λ + 2) (λ + 3) = 0, the eigen values are
Lag compensation permits a high gain at low frequencies.
If the poles lie in second quadrant, damping ratio is
Assertion (A): When performance specifications are given in term of transient response characteristics, root locus method is a suitable method.
Reason (R): When performance specifications in terms of state variables are given, modern control methods can be used.
If 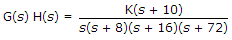 , the closed loop pole will be located at s = -12 when K =
, the closed loop pole will be located at s = -12 when K =
The sensor generally used in incremental optical encoder is
In terms of ξ and ωn the settling time of a second order systems for 2% criterion and step input is equal to
For 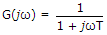 as ω approaches infinity, the magnitude approaches zero and phase angle approaches - 90�.
as ω approaches infinity, the magnitude approaches zero and phase angle approaches - 90�.
In the given figure, the combinations of two non touching loops is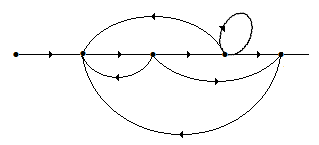
Nyquist stability criterion uses open loop frequency response characteristics.
For any test point s on the real axis, the sum of angular contributions of the complex conjugate poles is
For the system in the given figure G varies slightly, the ratio of open loop sensitivity to closed loop sensitivity is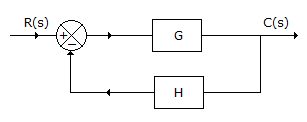
The loop transfer function of a feedback system is 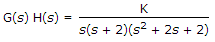 . The number of asymptotes of its root loci are
. The number of asymptotes of its root loci are
Which of the following can act as error detecting devices
- a pair of potentiometers
- a pair of synchros
- a differential transformer
- a metadyne
- a control transformer
Assertion (A): If minimum phase system has a gain margin of 8 dB and phase margin of 21º, the system is stable.
Reason (R): For a minimum phase system both GM and PM must be positive for the system to be stable.
For 0 < M < 1, the centres of M circle lie to the right of origin.
Assertion (A): Integration in time domain is converted into division in s domain
Reason (R): 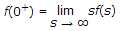
Assertion (A): In root locus the breakaway and break in points either lie on real axis or occur in complex conjugate pairs.
Reason (R): All root locus asymptotes intersect on real axis.
A conditionally stable system is stable for the value of gain between two critical values. It is unstable if














