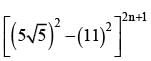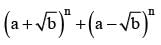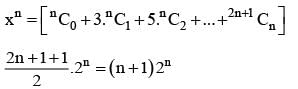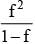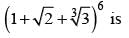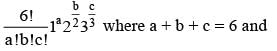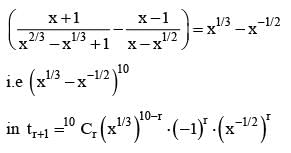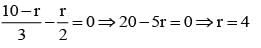Test: Binomial Theorem - 4 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Binomial Theorem - 4
The coefficients of 9th, 10th and 11th terms in the expansion of (1 + x)n are in A.P. then n =
The sum of the coefficient of even powers of x in the expansion (1 - x + x2 - x3)5 is
The number of terms in the expansion of [a + 4b)3 + (a + 4b)3]2 are
The sum of the binomial coefficients of the 3rd, 4th terms from the beginning and from the end of (a + x)n is 440 then n =
If 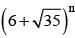 = I + F when I is odd and 0 < F < 1, then (I + F) (I - F) =
= I + F when I is odd and 0 < F < 1, then (I + F) (I - F) =
The expansion [x + (x3 - 1)1/2]5 + [x + (x3 - 1)1/2]5 is a polynomial of degree
If t0, t1, t2, ............tn are the consecutive terms in the expansion (x + a)n then (t0 - t2 + t4 - t6 +...)2 + (t1 - t3 + t5....)2 =
Coefficient of x50 in (1 + x)1000 + 2x(1 + x)999 + 3x(1 + x)998 + .....is
The coefficient of x9 in (x + 2) (x + 4) (x + 8).....(x + 1024) is
The coefficient of xn in the polynomial (x + nC0) (x + 3.nC1) (x + 5.n C2)... [x + (2n + 1).nCn] is
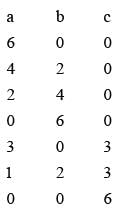
The coefficient of the term independent of x in the expansion of 
|
27 docs|150 tests
|


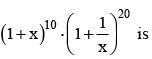
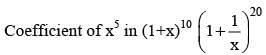

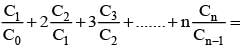

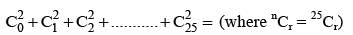
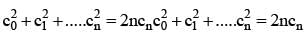

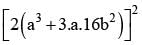
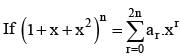 then a1 - 2a2 + 3a3 - ... - 2na2n = ....
then a1 - 2a2 + 3a3 - ... - 2na2n = ....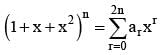
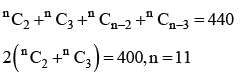
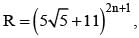 f = R - [R], then Rf =
f = R - [R], then Rf =