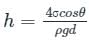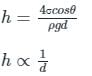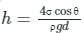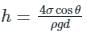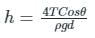Test: Capillary Action - Civil Engineering (CE) MCQ
10 Questions MCQ Test Fluid Mechanics for Civil Engineering - Test: Capillary Action
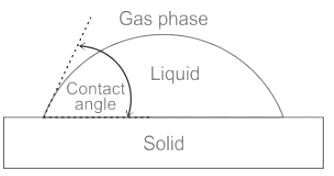
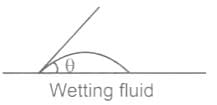
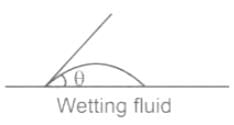
In which of the following conditions does the wettlng of surface usually occur
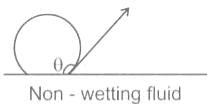
Due to which property of mercury, it does NOT stick to glass?
A capillary tube in a one-ton R22 air conditioner has a bore of 2⋅3 mm. Saturated liquid from the condenser enters at a temperature of 48°C and flows adiabatically through the tube until its temperature is 5°C. The friction factor is given as f = 0⋅32 / Re0⋅25. What is the length of the capillary tube? (Take intermediate sections at 40°C, 30°C, 20°C and 10°C and the mass flow rate of the refrigerant as 0⋅02417 kg/s)
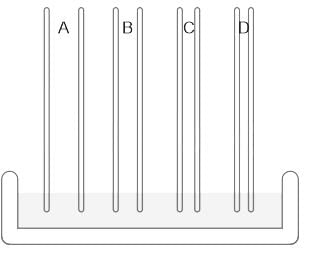
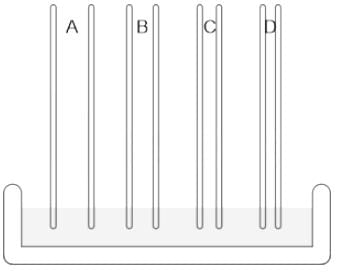
If you are given five samples of a liquid having a fixed density, identify the increasing order of the heights the samples will reach in the following capillary tubes.
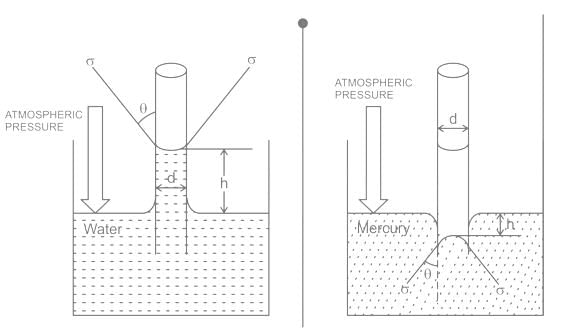
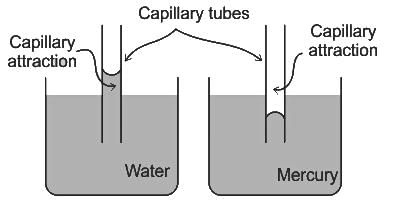
If one of the ends of the glass capillary tube is immersed in a liquid with stronger adhesion than cohesion then:
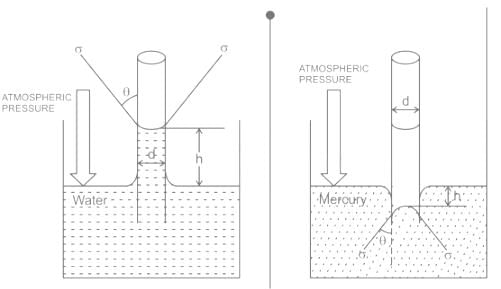
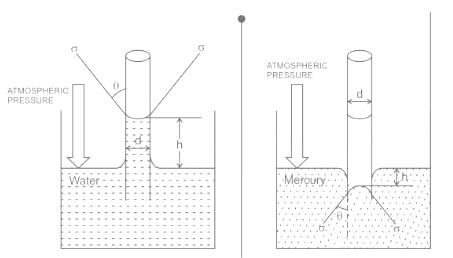
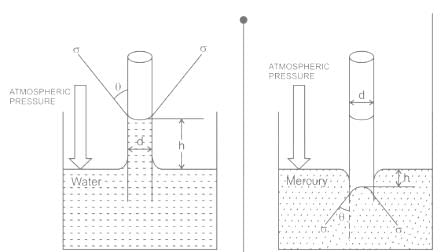
For water is rising in a capillary tube made of pure glass, what is the angle of contact?
Fluid rise in thin capillaries, also known as capillary action, is the virtue of which fluid property?
From the following sets of statements on capillary action, identify the correct pair.
I. Capillary effect is also known as meniscus effect.
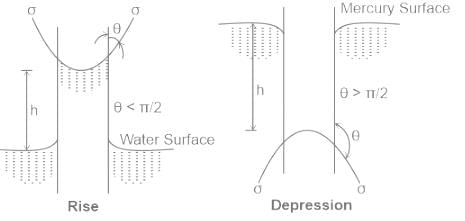
II. The fall of liquid surface during capillary action is known as capillary depression
III. The effect is represented in terms of mm/kg of liquid.
IV. The value of capillarity strictly depends only on specific weight of the liquid
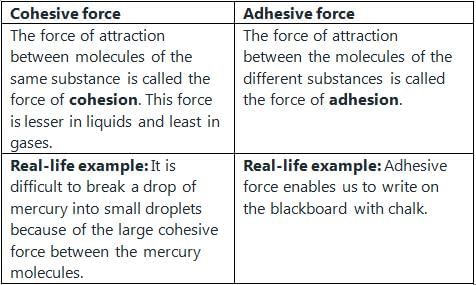
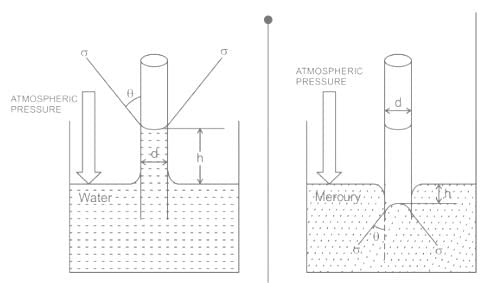
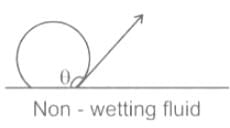
The phenomenon of rise or fall of liquid level in a capillarity tube is called as capillarity. In non-wetting liquids (e.g. mercury), what is the relation between cohesion of mercury and adhesion between mercury and capillary tube?
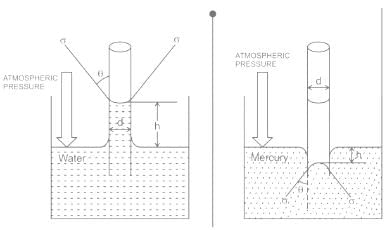
In order to avoid a correction for the effect of capillarity in manometers used for measuring pressure, the diameter of the tube should be:
|
54 videos|97 docs|110 tests
|


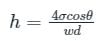

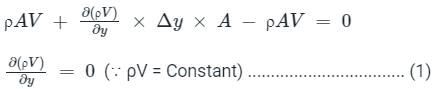
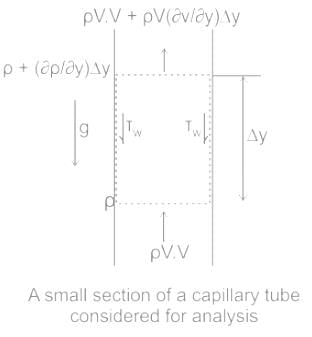
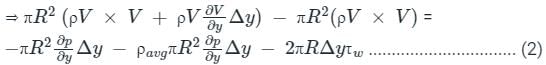
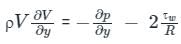 .......(3)
.......(3)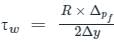 .........(4)
.........(4)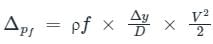 .........(5)
.........(5)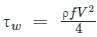 ...........(6)
...........(6)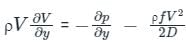 ..........(7)
..........(7)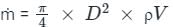
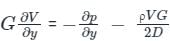 ...........(9)
...........(9)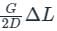 .......(10)
.......(10)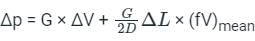 .........(11)
.........(11)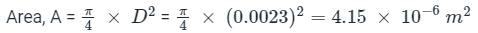
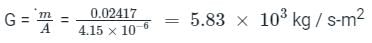
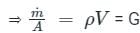 ...................... (12)
...................... (12)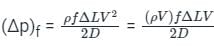
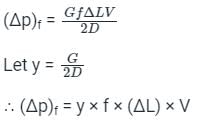
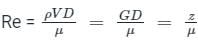
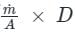 = 5.83 × 103 × 0.0023 = 13.409 Kg-s-1-m-1
= 5.83 × 103 × 0.0023 = 13.409 Kg-s-1-m-1