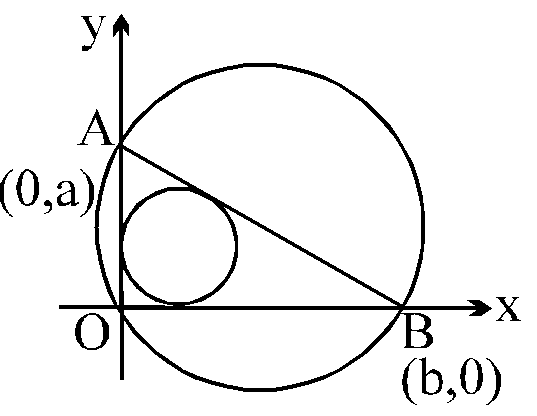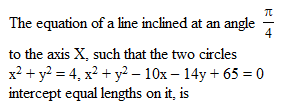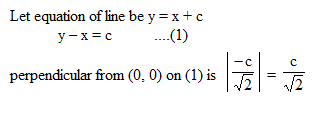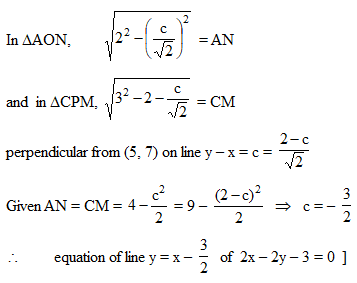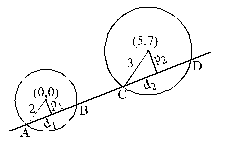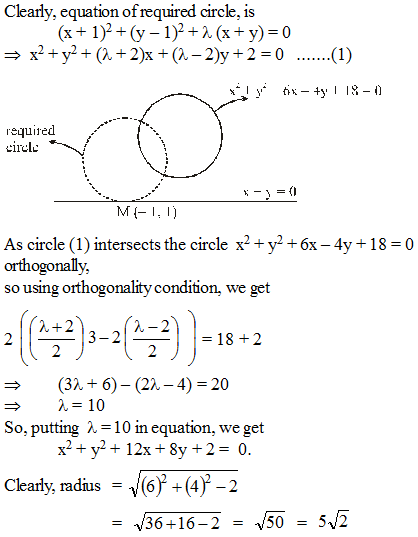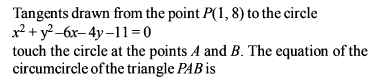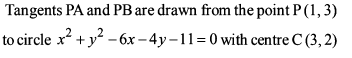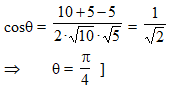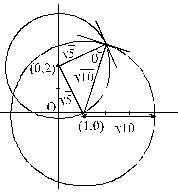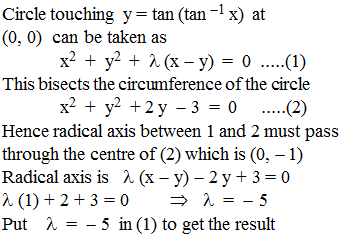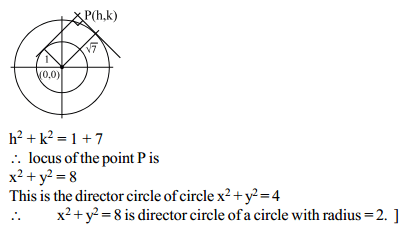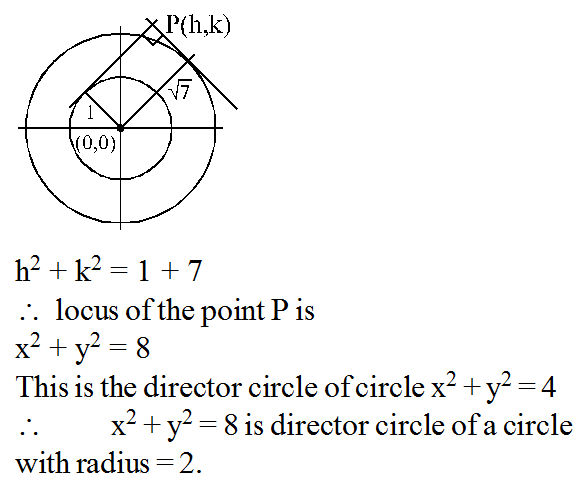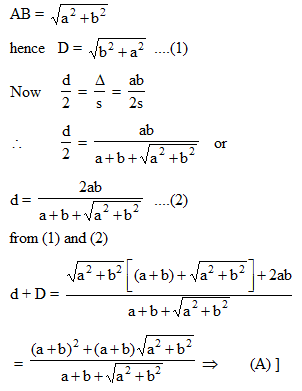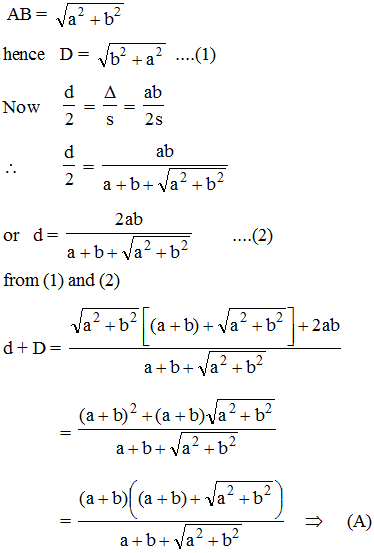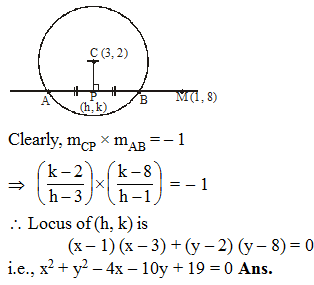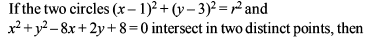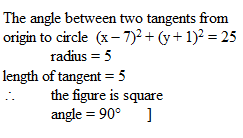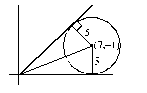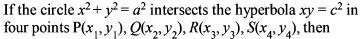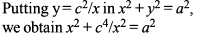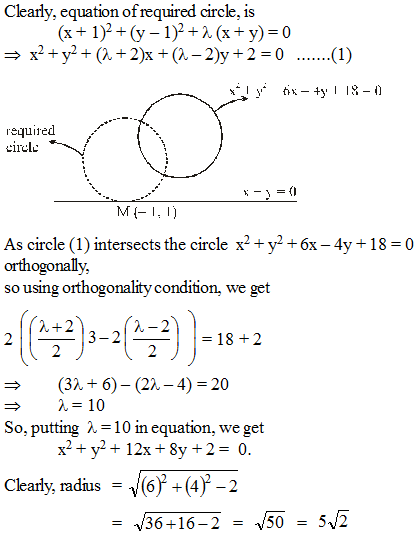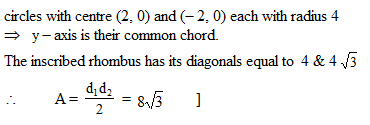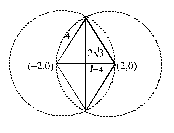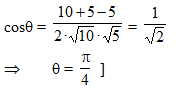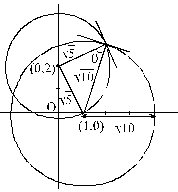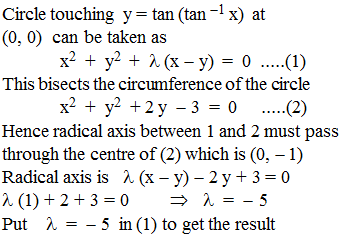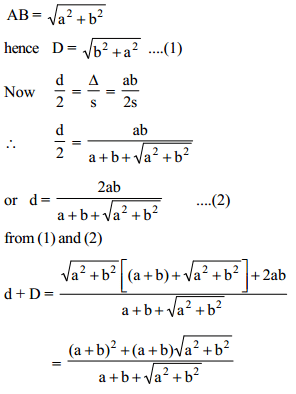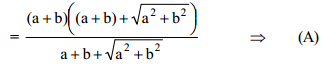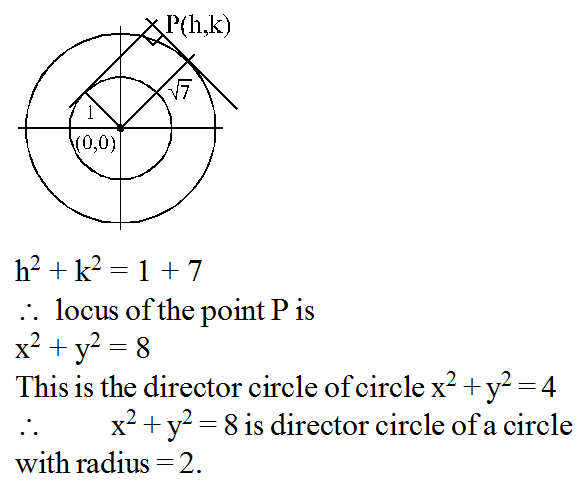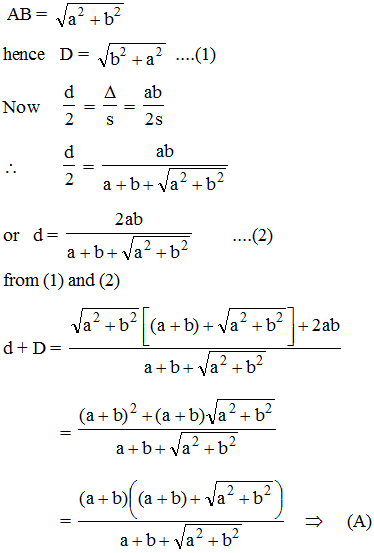Test: Circle - 5 - JEE MCQ

The angle at which the circles (x – 1)² + y² = 10 and  x² + (y – 2)² = 5 intersect is

Equation of the circle which bisects the circumference of the circle  x² + y² + 2 y - 3 = 0 and touches the curve    y = tan (tan^–1 x)  at the origin is :

Locus of the point of intersection of the pair of perpendicular tangents to the circles x² + y² = 1 and x² + y² = 7 is the director circle of the circle with radius.

Locus of the point of intersection of the pair of perpendicular tangents to the circles x² + y² = 1 and x² + y² = 7  is the director circle of the circle with radius.

Let a and b represent the length of a right triangle's legs. If d is the diameter of a circle inscribed into the triangle, and D is the diameter of a circle superscribed on the triangle, then d + D equals

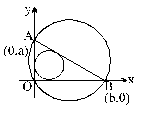
Let a and b represent the length of a right triangle's legs. If d is the diameter of a circle inscribed into the triangle, and D is the diameter of a circle superscribed on the triangle, then d + D equals

The possible radius of a circle whose centre is at the origin and which touches the circle x² + y² – 6x – 8y + 21 = 0, is

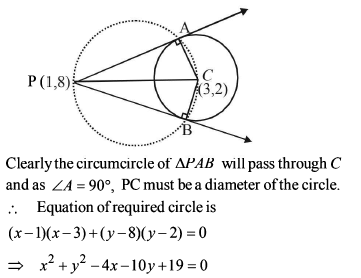
The locus of the midpoints of the chords drawn from the point M (1, 8) to the circle  x² + y² – 6x – 4y – 11 = 0, is equal to

The  angle  between the two tangents from the origin to the circle  (x - 7)² + (y + 1)² = 25 equals

The radius of  the circle which touches the line  x + y = 0 at M (– 1, 1) and cuts the circle   x² + y² + 6x – 4y + 18 = 0  orthogonally, is 

A rhombus is  inscribed  in  the  region  common to the two circles  x² + y² - 4x - 12 = 0  and x² + y² + 4x - 12 = 0  with two of its vertices on the line joining the centres of the circles. The area of  the  rhombous is  :

The angle at which the circles (x – 1)² + y² = 10 and  x² + (y – 2)² = 5 intersect is

Equation of the circle which bisects the circumference of the circle  x² + y² + 2 y - 3 = 0 and touches the curve    y = tan (tan^–1 x)  at the origin is :

Let a and b represent the length of a right triangle's legs. If d is the diameter of a circle inscribed into the triangle, and D is the diameter of a circle superscribed on the triangle, then d + D equals

Locus of the point of intersection of the pair of perpendicular tangents to the circles x² + y² = 1 and x² + y² = 7  is the director circle of the circle with radius.

Let a and b represent the length of a right triangle's legs. If d is the diameter of a circle inscribed into the triangle, and D is the diameter of a circle superscribed on the triangle, then d + D equals