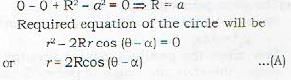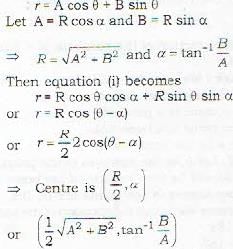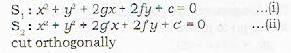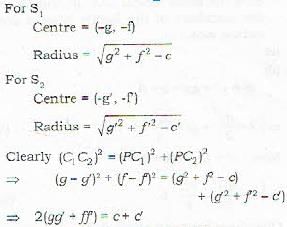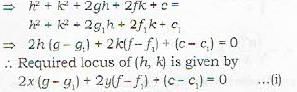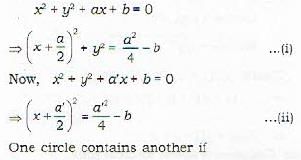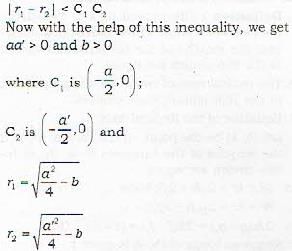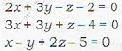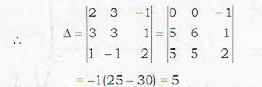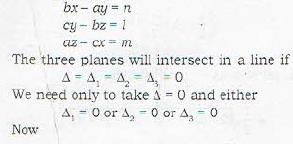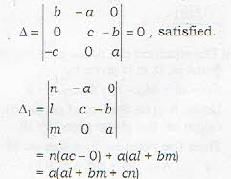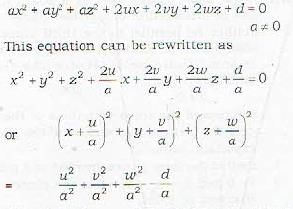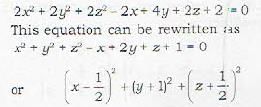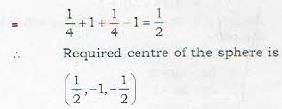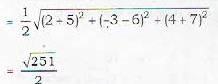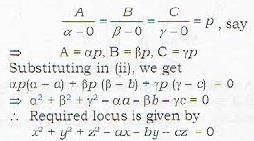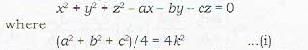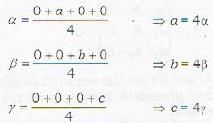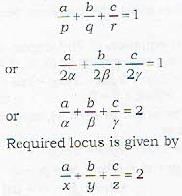Test: Dimensional Geometry - 10 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Dimensional Geometry - 10
The polar equation of a circle with centre (R, α), radius a and passing through the pole, is given W
The coordinates of the centre of a circle r = A cos θ + B sinθ are given by
The equation of the tangent to the circle r = 2a cosθ at any point (r1, θ1) is given by-
The circles x2 + y2 + 2px + 2fy + c = 0 and x2 y2 + 2g' + 2f'y - c = 0 cut each other orthogonally if
The radical axis of the two circles
x2 + y2 +2gx + 2fy + c = 0 and
x2 + y2 + 2g1x + 2f1y + c1 =0 is given by
Centre of all the three circles of a co-axial system
One of two circles
x2 + y2 + ax + b = 0
and x2 + y2 + a'x + b = 0
will be within the other
The three planes
2x + 3y - z - 2 = 0
3x + 3y + z - 4 - 0
x - y + 2z - 5 = 0
intersect in
The planes bx - ay = n, cy - bz = l, az - cx = m intersect in a line if
The equation
ax2 + ay2 + az2 + 2ux - 2vy - 2wz + d - 0 (a ≠ 0)
represents a sphere if
The centre of the sphere
2x2 + 2y2 + 2z2 - 2x + 4y + 2z + 3 = 0 is
The radius of the sphere described on the join of (2, -3, 4) and (-5, 6, -7) as diameter is
The locus of the foot of the perpendicular drawn from the origin to a plane passing through a fixed point (a, b, c) is
A sphere of constant radius 2k passes through the origin and meets the axes in A, B, C. The locus of the centroid of tetrahedron OABC is
Which of the following statements is wrong? The equatioin x2 + y2 + z2 - ax - by - cz = 0 represents the
A plane passes through a fixed point (a, b, c) and cuts the axes in A, B and C. Then the locus of the centre of the sphere passing through the origin and the points A, B and C is given by
Which of the following is a correct statement?
The circle is
|
27 docs|150 tests
|