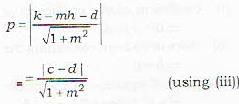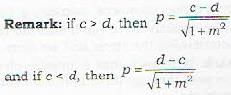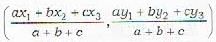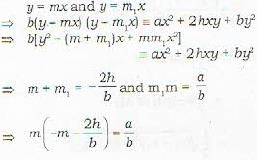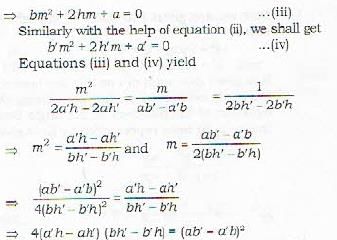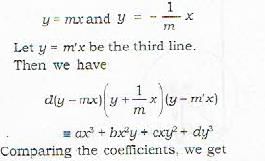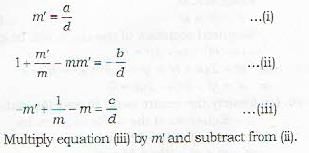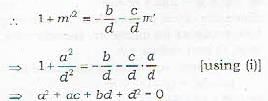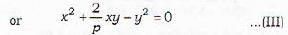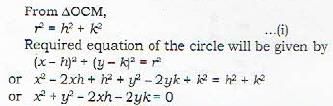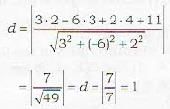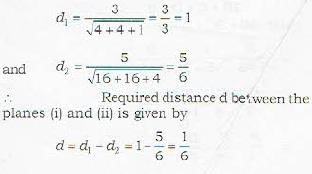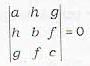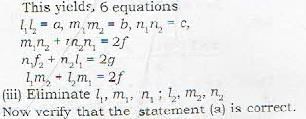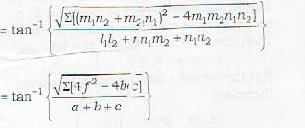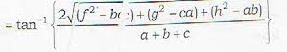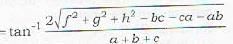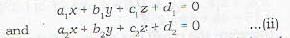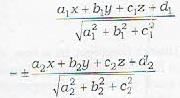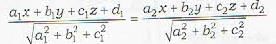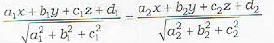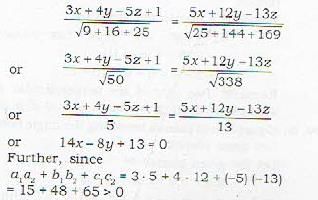Test: Dimensional Geometry - 7 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Dimensional Geometry - 7
The diagonals of a parallelogram whose sides are given by
√3x + y = 0, √3y + x = 0
√3x + y = 1, √3y + x = 1
are inclined ai an angle of ... to one anothe
√3x + y = 0, √3y + x = 0
√3x + y = 1, √3y + x = 1
are inclined ai an angle of ... to one anothe
The distance between the two parallel straight lines
y = mx - c and y = mx + d is given by
y = mx - c and y = mx + d is given by
Let ABC be a given triangle the coordinates of whose vertices are given by (x1,y1), (x2,y2) and (x3,y3) respectively. Then the coordinate of the centre of the circle inscribed in it (where a, b, c represent the sides BC, CA and AB respectively) are given by
The equation of the two straight lines joining the origin to the points of intersection of the straight line lx + my + n = 0 and the curve
ax2 + 2hxy - by2 + n = 0 and the curve
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 is given by
The condition that one of the straight lines given by the equation ax2 + 2hxy + by2 = 0 may coincide with one of those given by the equation a'x2 + 2h'xy - b'y2 = 0 is given b
The two straight lines represented by the equation ax2 + bx2y + cxy2 + dy = 0 are at right angles if
If each of the pairs of straight lines x2 - 2pxy - y2 = 0 and x2 - 2qxy- y2 = 0 bisects the angles between the other pair, then
The equation of te circle whose centre is (h, k) and which passes through tire origin, is given by
The equation of the circle whose centre lies on x-axis at a distance h from the origin and radius is a, is given by
The equation of the circle, passing through the origin such that the x-axis is its diameter, is given by
The distance of the point (2, 3, 4) from the plane 3x - 6y + 2z + 11 =0 is
The distance between the parallel planes 2x -2y + z + 3 = 0 and 4x -4y + 2z + 5 = 0 is
The equation
ax2 + by2 + cz2+ 2fyz + 2gzx + 2hxy = 0
represents a pair of planes if
The two planes represented by ax2 - by2 + cz2 + 2fyz + 2gzx + 2 hxy = 0 are perpendicular if
Which of the following equation represent pair of perpendicular planes?
The equation of the bisector of the angle between two planes a1x + b1y + c1z +d1 = 0 and a2x + b2y + c2z + d2 = 0
containing the origin is given by
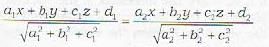 provided
provided
14x - 8y - 13 = 0 is the equation of bisector of the angle between the planes
3x + 4y - 5z + 1= 0, 5x + 12y - 13z = 0
The volume of the tetrahedron, the coordinates of whose vertices are (x1, y1, z1) , (x2, y2, z2), (x3, y3, z3) and (x4, y4, z4 ) is given by 
A straight line is represented by .... equations of the first degree in x, y, z
A given iine can be represented by how many pairs of first degree equations in x,y,z?
|
27 docs|150 tests
|