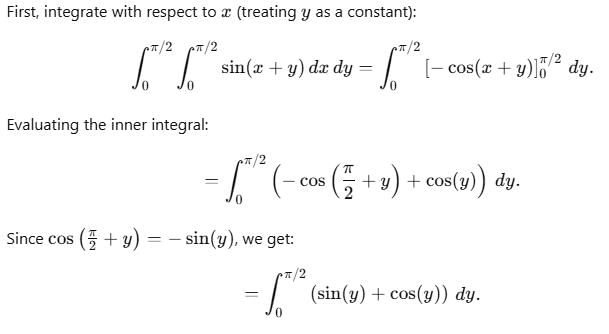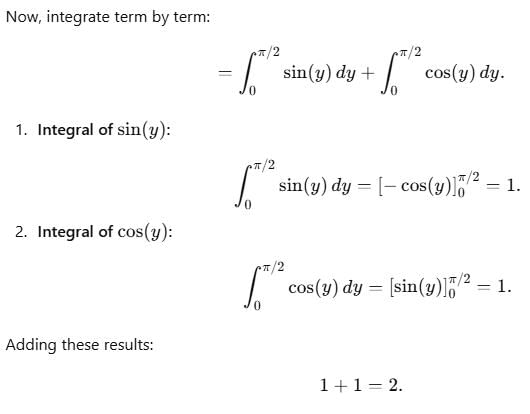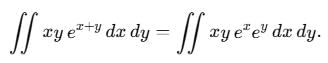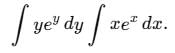Test: Double And Triple Integrals - 1 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Double And Triple Integrals - 1
The value of 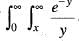 dxdy changing the order of integration is
dxdy changing the order of integration is
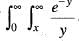 dxdy changing the order of integration is
dxdy changing the order of integration is The area bounded by the curve y = ψ(x), x-axis and the lines x = l , x = m(l <m ) is given by
The volume of an object expressed in spherical coordinates is given by 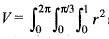 sin φ dr dφ dθ. The value of the integral is
sin φ dr dφ dθ. The value of the integral is
Using the transformation x + y = u, y = v. The value of Jacobian (J) for the integral 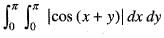 is
is
The area bounded by the parabola y2 = 4ax and straight line x + y = 3a is
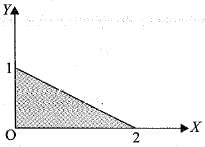
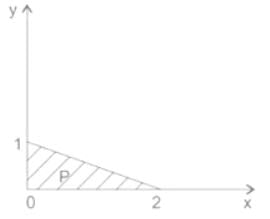
Consider the shaded triangular region P shown in the figure, what is the value of 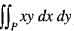 ?
?
To evaluate 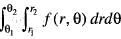 over the region A bounded by the curve r = r1, r = r2 and the straight lines θ = θ1, θ = θ2, we first integrate
over the region A bounded by the curve r = r1, r = r2 and the straight lines θ = θ1, θ = θ2, we first integrate
To change Cartesian plane (x, y, z) to spherical polar coordinates (r, θ, φ)
If the triple integral over the region bounded by the planes 2x + y + z = 4, x = 0, y = 0, z = 0 is given by then the function λ(x) – π(x, y) is
Area bounded by the curves y2 = x3 and x2 = y3 is
By changing the order of integration in 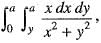 the value is
the value is
By the change of variable x(u, v) = uv, y(u, v) = u/v is double integral, the integrand f(x, y) change to 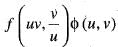 . Then, φ(u,v) is
. Then, φ(u,v) is
The volume of the tetrahedron bounded by the plane 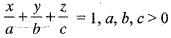 and the co-ordinate planes is equal to
and the co-ordinate planes is equal to
|
27 docs|150 tests
|


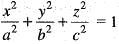 is
is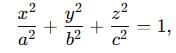
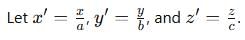
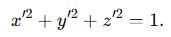
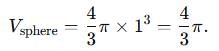
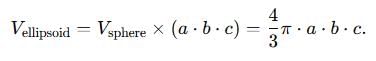
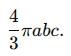

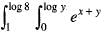 dx dy is equal to
dx dy is equal to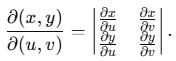
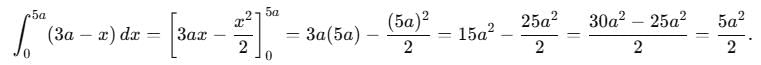
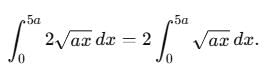
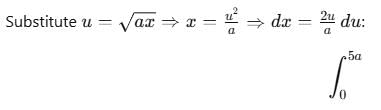
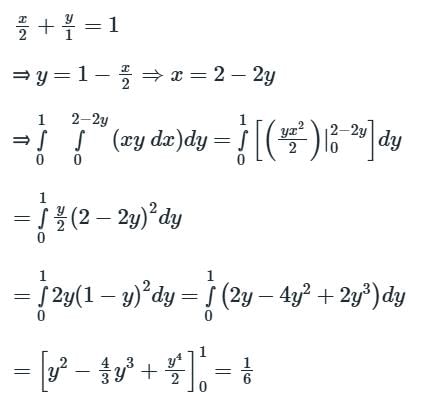
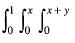 (x + y + z) dz dy dx is
(x + y + z) dz dy dx is 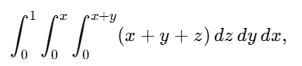




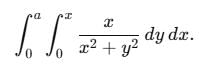
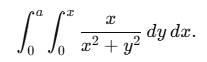
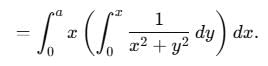

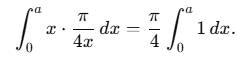
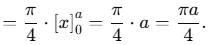
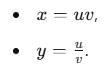


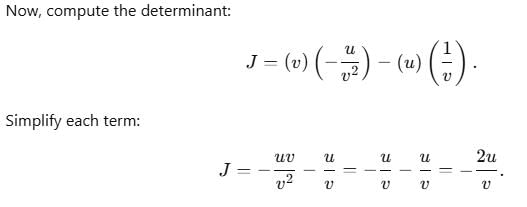
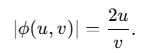
 abc du dv dw
abc du dv dw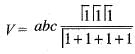
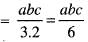
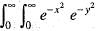 dxdy is
dxdy is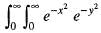 dxdy
dxdy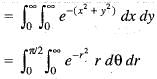
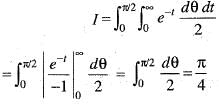
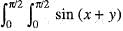 dxdy is
dxdy is