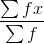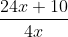Test: Elementary Mathematics - 1 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2025 - Test: Elementary Mathematics - 1
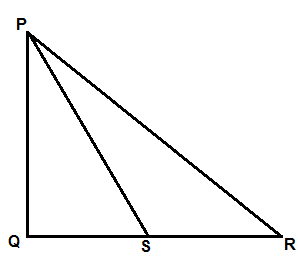
Directions: In right-angled triangle PQR, which is right angled at Q, S is the mid-point of QR.
Which one of the following is correct?
If x = 111...1 (20 digits), y = 333...3 (10 digits) and z = 222...2 (10 digits), then 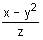 is equal to
is equal to
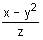 is equal to
is equal toConsider the following statements:
Statement I: The value of a random variable having the highest frequency is mode.
Statement II: Mode is unique.
Which of the following options is correct in respect of the above statements?
25 kg of alloy X is mixed with 125 kg of alloy Y. If the amount of lead and tin in the alloy X is in the ratio 1 : 2 and the amount of lead and tin in the alloy Y is in the ratio 2 : 3, then what is the ratio of lead to tin in the mixture?
Consider the following statements:
1. If 45°< x < 60°, then sec2x + cosec2x = y2 for some real number y > 1.
2. If 0° < x < 45°, then 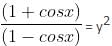 for some real number y > 2.
for some real number y > 2.
3. If 0° < x < 45°, then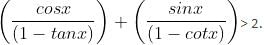
What is the number of true statements?
If ax = b, by = c and cz = a, find the value of xyz.
The condition that the roots of the equation px2 + qx + r = 0 are the reciprocals of the roots of equation ax2 + bx + c = 0 is
What is the approximate ratio of number of eatables produced by company A to that produced by company C?
The total population of males of UP, MP and Goa taken together is what percent of the total population of all the given states?
What was the total number of illiterate people in AP and MP?
What is the ratio of the number of females in Tamil Nadu to that in Delhi?
What percentage of consumption needs to be reduced if the price is raised by 12%, but the expenditure is to be the same?
If cosθ1 + cosθ2 + cosθ3 = 3, then what is sinθ1 + sinθ2 + sinθ3 equal to?
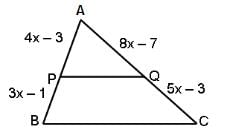
In triangle ABC, BC is parallel to PQ. Find the value of x.
In a 100 m race, A runs at 6 km/hr. If A gives B a start of 8 m and still beats him by 9 seconds, what is the speed of B?
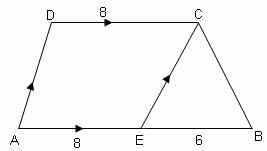
In the figure shown below, AB is parallel to DC and the lengths of line segments are marked. The area of ΔCEB is 12 sq units. What is the area of the quadrilateral ABCD in sq units?
If x = a cosθ + b sinθ and y = a sinθ – b cosθ, then what is x2 + y2 equal to?
30 men can complete a job in 40 days. However, after 24 days some men out of the assigned 30 left the job. The remaining people took another 40 days to complete the job. The number of men who left the job is
Which of the following options is necessarily true if f(x) = x3 - 4x + p and f(0) and f(1) have opposite signs?
A sum of Rs. 8,400 is taken as a loan. This is to be paid in two equal installments. If the rate of interest is 10% per annum, compounded annually, then the value of each installment is
The compound interest on a sum for 2 years is Rs. 832 and simple interest on the same sum at the same rate for the same period is Rs. 800. What is the rate of interest?
The frequencies of the digits 3, 5, 7 and 9 are x - 2, x + 2, x - 3 and x + 3, respectively. If their arithmetic mean is 6.5, find the value of x.
|
33 docs|73 tests
|


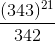 ] = Rem[
] = Rem[ ] = Rem[1/342] = 1
] = Rem[1/342] = 1

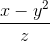 is equal to 1.
is equal to 1.

 75 = Sum
75 = Sum The number that was added later
The number that was added later
 102 = 75 + R
102 = 75 + R

 = 60
= 60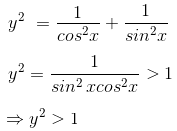
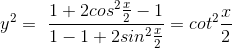
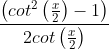

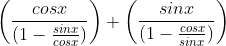
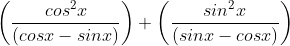

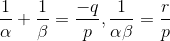
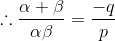
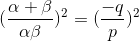
 x 100 = (567/20) x 100 = 28.35%.
x 100 = (567/20) x 100 = 28.35%. =
=  = 15/14
= 15/14 is not a real number. So, option (4) is not true.
is not a real number. So, option (4) is not true.
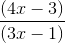 =
= 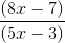
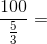 60 seconds
60 seconds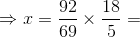 4.8 km/hr
4.8 km/hr
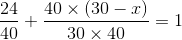
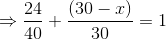
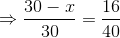
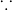 f(0) and f(1) have opposite signs
f(0) and f(1) have opposite signs M + 2 = 3S + 6
M + 2 = 3S + 6 M - 3S = 4 ……(2)
M - 3S = 4 ……(2) M - 4S = -6
M - 4S = -6 M - 3S = 4
M - 3S = 4

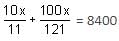


 …(i)
…(i)

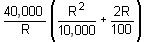
 = 300%
= 300%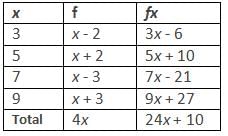
 =
=