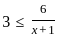Test: Elementary Mathematics - 5 - CDS MCQ
30 Questions MCQ Test - Test: Elementary Mathematics - 5
If logax x, logbx x, logcx x are in H.P., where a, b, c, x belong to (1, ∞), then a, b, c are in
If x2 - 15x + 1 = 0, what is the value of x4 - 223x2 + 6?
If the equation k(21x2 + 24) + rx + (14x2 − 9) = 0
k(7x2 + 8) + px + (2x2 − 3) = 0 have both roots common, then the value of P/r is:
Anu had 8 packets of 36 toffees each to distribute on her birthday. She distributed 1/4 of the toffees among her friends and 3/8 among her teachers. She kept 1/3 of the toffees for her brother. How many toffees are left with her now?
Let x = (633)24 – (277)38+ (266)54. What is the units digit of x?
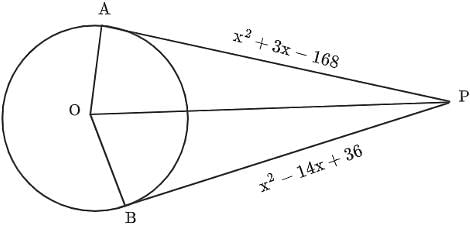
In the given figure, two tangents are drawn from a point P to a circle. The tangents PA and PB touch the circle at points A and B, respectively. The length of the line segment OP is 13 cm, where O is the centre of the circle. Then find the radius of the given circle.
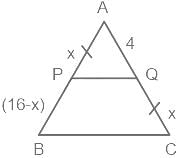
In Δ ABC, the straight line parallel to the side BC meets AB and AC at the points P and Q. respectively. If AP = QC, the length of AB is 16 cm and the length of AQ is 4 cm, then the length (in cm) CQ is:
If x = log2a a, y = log3a 2a and z = log4a 3a, then xyz + 1 =
The mean and standard deviation of 75 observations are 45 and 10, respectively. If 2 is added to each observation, the new mean and standard deviation will be
If x2 - 5x - 14 > 0 ⟹ x lie outside [α , β], then α/β =
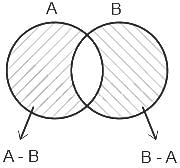
If A and B are two sets, then
(A - B) U (B - A) U (A ∩ B) is equal to
If X = {8n - 7n - 1 : n ∈ N} and
Y = {49 (n - 1) : n ∈ N}, then
If A = {(x, y) : x2 + y2 ≤ 1, x, y ∈ R) and
B = {(x, y): x2 + y2 ≤ 4; x, y ∈ R), then
The numerator and denominator of a fraction are in the ratio 2 ∶ 3. If 6 is subtracted from the numerator, the result is a fraction whose value is 2/3 that of the real fraction. The numerator of the real fraction is
If 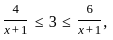 where (x > 0); then the possible value of x can be.
where (x > 0); then the possible value of x can be.
If the ratio of mean and median of a distribution is 2 : 3 then the ratio of mode and mean is



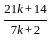 =
= 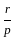 =
= 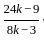
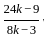
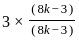
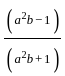 .
.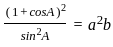
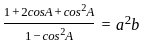 __________Eqn 1
__________Eqn 1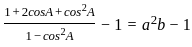
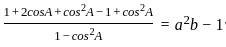
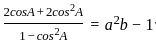
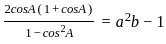 ________Eqn 2
________Eqn 2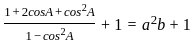
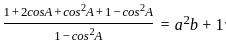
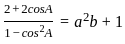
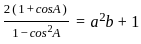 _______ Eqn3
_______ Eqn3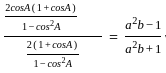
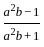
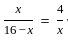
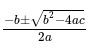
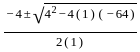
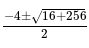
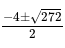
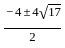
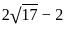
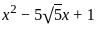 = 0, and x > 0, what is the value of
= 0, and x > 0, what is the value of 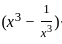 ?
?
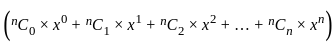
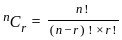
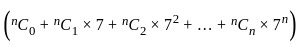 - (7n + 1)
- (7n + 1)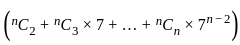
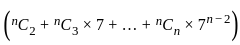
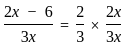
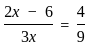
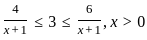
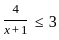 we get
we get