All Courses
Get the App Signup / Login
Sign in Open App
Mechanical Engineering Exam  >  Mechanical Engineering Tests  >  Fluid Mechanics for Mechanical Engineering  >  Test: Fluid Kinematics Level - 1 - Mechanical Engineering MCQ

Test: Fluid Kinematics Level - 1 - Mechanical Engineering MCQ


Test Description

15 Questions MCQ Test Fluid Mechanics for Mechanical Engineering - Test: Fluid Kinematics Level - 1

Test: Fluid Kinematics Level - 1 for Mechanical Engineering 2024 is part of Fluid Mechanics for Mechanical Engineering preparation. The Test: Fluid Kinematics Level - 1 questions and answers have been prepared according to the Mechanical Engineering exam syllabus.The Test: Fluid Kinematics Level - 1 MCQs are made for Mechanical Engineering 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Fluid Kinematics Level - 1 below.
Solutions of Test: Fluid Kinematics Level - 1 questions in English are available as part of our Fluid Mechanics for Mechanical Engineering for Mechanical Engineering & Test: Fluid Kinematics Level - 1 solutions in Hindi for Fluid Mechanics for Mechanical Engineering course. Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free. Attempt Test: Fluid Kinematics Level - 1 | 15 questions in 20 minutes | Mock test for Mechanical Engineering preparation | Free important questions MCQ to study Fluid Mechanics for Mechanical Engineering for Mechanical Engineering Exam | Download free PDF with solutions
Test: Fluid Kinematics Level - 1 - Question 1
Save

A steady, incompressible, two–dimensional velocity field is given by V‾ = (u, v) = (0.5 + 0.8x)î + (1.5 − 0.8 y)ĵ The number of stagnation points in the flow field is

Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 1
Stagnation points are those points where (u, v) = 0

u = 0.5 + 0.8x = 0

∴ x = −0.5 / 0.8 = −0.625

v = 1.5 − 0.8y = 0

∴ y = 1.5 / 0.8 = 1.875

i.e there is only one stagnation point at (−0.625, 1.875)

Test: Fluid Kinematics Level - 1 - Question 2
Save

A stream function is given by ψ = 4x − 3y. The magnitude of resultant velocity at any point is

Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 2
Given, ψ = 4x − 3y

As per definition of stream function

u = ∂ψ / ∂y and v = −∂ψ / ∂x

∴ u = −3 & v = −4 So V- = −3î − 4ĵ

and magnitude of resultant velocity is given |⃗V⃗ | = √u2 + v2 = 5

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Fluid Kinematics Level - 1 - Question 3
Save

Match List-I (Pipe flow) with List-II (Type of acceleration) and select the correct answer.

List-I List-II

a. Flow at constant rate through a bend 1. Zero acceleration

b. Flow at constant rate through a 2. Local and convective acceleration

straight uniform diameter pipe

c. Gradually changing flow through a bend 3. Convective acceleration

d. Gradually changing flow through a straight pipe 4. Local acceleration

Codes:

a b c d

Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 3
For flow through bends, the direction of velocity changes as the fluid moves through the bend but since the flow rate is constant, and if cross-section is uniform the flow is steady, hence only convective acceleration exists.

Similarly for constant flow rate through a straight, uniform diameter pipe, there is no change of velocity, (neither magnitude nor direction) so total acceleration is zero.

For a flow through bend where the discharge is not constant, the velocity changes both due to geometry of pipe and with time, so both local and convective acceleration exist.

For variable discharge through a straight pipe, the velocity will change with time, but it will be same across the whole pipe at any particular time instant, i.e the flow is unsteady but uniform, only local acceleration exists.

Test: Fluid Kinematics Level - 1 - Question 4
Save

Which one of the following stream functions represents a possible irrotational flow field?
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 4
For irrotational flow, stream function must satisfy Laplace equation i.e

∂2ψ / ∂x2 + ∂2ψ / ∂y2 = 0

Checking all the given options, we find option (A) satisfies the equation.

Test: Fluid Kinematics Level - 1 - Question 5
Save

The velocity potential function for a two dimensional flow field is given by ϕ = x2 − y2. The magnitude of velocity at the point (1,1) is
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 5
ϕ = x2 − y2

we know u = −∂ϕ / ∂x and v = −∂ϕ / ∂y

∴ u = −(2x), v = −(−2y)

⇒ u = −2x, v = 2y

Thus at (1, 1),⃗V⃗ = −2î + 2ĵ |⃗V⃗ | = √4 + 4 = 2 × 21/2

Test: Fluid Kinematics Level - 1 - Question 6
Save

Pipe 1, branches into three pipes as shown in the given figure. The areas and corresponding velocities are as given in the following table the value of V2 in cm per second will be

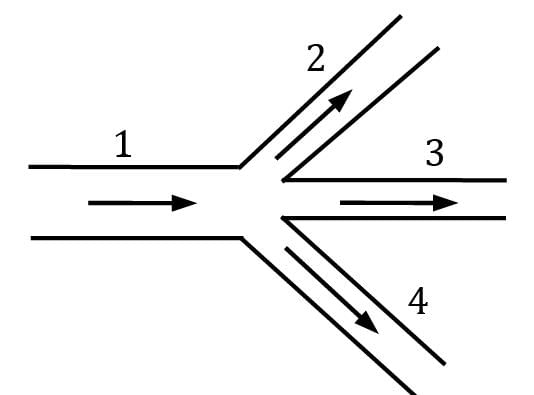
Pipe Velocity (cm per second) Area (sq. cm)
1. 50 20
2. V2 10
3. 30 15
4. 20 10

Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 6

For incompressible fluid, A1V1 = A2V2 + A3V3 + A4V4

1000 = 10 V2 + 450 + 200

V2 = 35 cm/s

Test: Fluid Kinematics Level - 1 - Question 7
Save

If the stream function for a 2D flow is given as ψ = 3xy, then the velocity at the point (2, 3) will be
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 7
Given, ψ = 3xy By definition of ψ

u = ∂ψ / ∂y and v = −∂ψ / ∂x

So u = 3x, v = −3y

at point (2, 3)

⃗V = 6î − 9ĵ and |⃗V⃗ | = √62 + 92 = 10.816

≈ 10.82 Units

Test: Fluid Kinematics Level - 1 - Question 8
Save

If the velocity potential function ϕ for a flow satisfies the Laplace equation δ2ϕ⁄δx2 + δ2ϕ⁄δy2 + δ2ϕ⁄δz2 = 0 then the flow is
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 8
Velocity potential function is defined only for irrotational flows, whether the flow is steady or unsteady, compressible or incompressible. If it also satisfies Laplace equation then the flow is also incompressible.

Test: Fluid Kinematics Level - 1 - Question 9
Save

Circulation is defined as the line integral of tangential component of velocity along a
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 9
Circulation is defined as the cyclic integral of tangential velocity about a closed loop.

Test: Fluid Kinematics Level - 1 - Question 10
Save

Which of the following flow is rotational? (where u and v are velocity components in x and y directions respectively)
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 10
For a 2D flow to be rotational

Ωz = 0

Checking option (A)

Ωz = ∂v / ∂x −∂u / ∂y =3/2 − 1 ≠ 0

Checking option (B)

Ωz = ∂v / ∂x −∂u / ∂y = 2xy − 2xy = 0

Test: Fluid Kinematics Level - 1 - Question 11
Save

For irrotational flow, the curl of velocity vector is
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 11
The curl of velocity vector represents the vorticity of flow, and for irrotational flow, the vorticity is zero. i.e curl of velocity = 0 for irrotational flow.

Test: Fluid Kinematics Level - 1 - Question 12
Save

A flow field satisfying ⛛.V‾= 0 as the continuity equation represents
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 12
For general flow, ∂ρ / ∂t + V- ∙ (ρV ) = 0 ⋯ ①

If ρ = C

i. e. ρ ≠ ρ(x, y, z, t)

Hence equation ① is reduced to V ∙⃗V = 0 for incompressible flow.

Test: Fluid Kinematics Level - 1 - Question 13
Save

A steady incompressible 2D flow field is given by u = 2x2 + y2 and v = −4xy. The convective acceleration along x-direction at point (1, 2) is
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 13
u = 2x2 + y2, v = −4xy

ax = (2x2 + y2)(4x) + (−4xy)(2y) + 0 + 0

∴ at point (1, 2) ax

= (2 + 4)(4) − (8)(4) ax

= 24 − 32 ax

= −8 units

Test: Fluid Kinematics Level - 1 - Question 14
Save

A two-dimensional flow field is defined as V‾ = xî − yĵ. The equation of the streamline passing through the point (1, 2) is
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 14
V = xî − yĵ

i. e u = x, v = −y

For a streamline in 2D flow,

dy / dx =v / u ⟹ dy / dx =−y /x

⇒ ln y = ln 1 / x + C

at (1, 2) ln 2 = ln 1 + C

C = ln 2

So, ln y = ln 2 / x

or xy = 2 or xy − 2 = 0

Test: Fluid Kinematics Level - 1 - Question 15
Save

In a two dimensional flow in x-y plane, if ∂u / ∂y = ∂v / ∂x , then the fluid element will undergo
Detailed Solution for Test: Fluid Kinematics Level - 1 - Question 15
For a 2D planar flow the deformation rate is given as ε̇ xy = ∂v / ∂x + ∂u / ∂y And rotation rate is given as

ωz = 1/[∂v / ∂x − ∂u / ∂y ]

Therefore in the given case ε̇ xy = 2 ∂u / ∂y and ωz = 0

Thus along with translation, elements will deform but shall not rotate.

56 videos|104 docs|75 tests
Join Course
Information about Test: Fluid Kinematics Level - 1 Page
In this test you can find the Exam questions for Test: Fluid Kinematics Level - 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Fluid Kinematics Level - 1, EduRev gives you an ample number of Online tests for practice

Top Courses for Mechanical Engineering

Download as PDF

Top Courses for Mechanical Engineering

Important Questions for Fluid Kinematics Level - 1

Find all the important questions for Fluid Kinematics Level - 1 at EduRev.Get fully prepared for Fluid Kinematics Level - 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Fluid Kinematics Level - 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Fluid Kinematics Level - 1 resources.

Fluid Kinematics Level - 1 MCQs with Answers

Prepare for the Fluid Kinematics Level - 1 within the Mechanical Engineering exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Fluid Kinematics Level - 1 Fluid Mechanics for Mechanical Engineering

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Fluid Kinematics Level - 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup