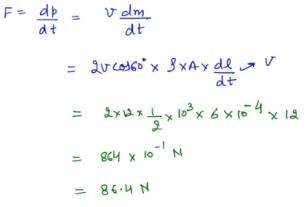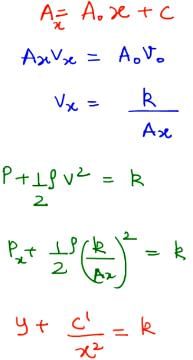Test: Fluid Mechanics - 1 - NEET MCQ
30 Questions MCQ Test Physics Class 11 - Test: Fluid Mechanics - 1
A bucket contains water filled upto a height = 15 cm. The bucket is tied to a rope which is passed over a frictionless light pulley and the other end of the rope is tied to a weight of mass which is half of that of the (bucket + water). The water pressure above atmosphere pressure at the bottom is :
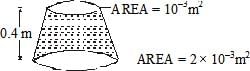
A uniformly tapering vessel shown in Fig. is filled with liquid of density 900 kg/m3. The force that acts on the base of the vessel due to liquid is (take
g = 10 m/s2) -
g = 10 m/s2) -
A liquid of mass 1 kg is filled in a flask as shown in figure. The force exerted by the flask on the liquid is (g = 10 m/s2)
[Neglect atmospheric pressure]

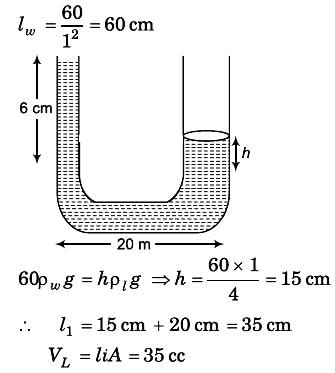
A U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area = 1 cm2. It is filled with water of volume 60 cc. What volume of a liquid of density 4 g/cc should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?
A light semi cylindrical gate of radius R is piovted at its mid point O, of the diameter as shown in the figure holding liquid of density r. The force F required to prevent the rotation of the gate is equal to
The pressure at the bottom of a tank of water is 3P where P is the atmospheric pressure. If the water is drawn out till the level of water is lowered by one fifth., the pressure at the bottom of the tank will now be
An open-ended U-tube of uniform cross-sectional area contains water (density 1.0 gram/centimeter3) standing initially 20 centimeters from the bottom in each arm. An immiscible liquid of density 4.0 grams/centimeter3 is added to one arm until a layer 5 centimeters high forms, as shown in the figure above. What is the ratio h2/h1 of the heights of the liquid in the two arms ?
The area of cross-section of the wider tube shown in figure is 800 cm2. If a mass of 12 kg is placed on the massless piston, the difference in heights h in the level of water in the two tubes is :
A body is just floating in a liquid (their densities are equal) If the body is slightly pressed down and released it will -
Two stretched membranes of areas 2 and 3 m2 are placed in a liquid at the same depth. The ratio of the pressure on them is -
An ice block floats in a liquid whose density is less than water. A part of block is outside the liquid. When whole of ice has melted, the liquid level will -
A fluid container is containing a liquid of density r is is accelerating upward with acceleration a along the inclined place of inclination a as shwon. Then the angle of inclination q of free surface is :
Figure shows a three arm tube in which a liquid is filled upto levels of height l. It is now rotated at an angular frequency w about an axis passing through arm B. The angular frequency w at which level of liquid of arm B becomes zero.
Two cubes of size 1.0 m sides, one of relative density 0.60 and another of relative density = 1.15 are connected by weightless wire and placed in a large tank of water. Under equilibrium the lighter cube will project above the water surface to a height of
A cuboidal piece of wood has dimensions a, b and c. Its relative density is d. It is floating in a larger body of water such that side a is vertical. It is pushed down a bit and released. The time period of SHM executed by it is :
Two bodies having volumes V and 2V are suspended from the two arms of a common balance and they are found to balance each other. If larger body is immersed in oil (density d1 = 0.9 gm/cm3) and the smaller body is immersed in an unknown liquid, then the balance remain in equilibrium. The density of unknown liquid is given by :
A boy carries a fish in one hand and a bucket (not full) of water in the other hand. If the places the fish in the bucket, the weight now carried by him (assume that water does not spill) :
A piece of steel has a weight W in air, W1 when completely immersed in water and W2 when completely immersed in an unknown liquid. The relative density (specific gravity) of liquid is :
A ball of relative density 0.8 falls into water from a height of 2m. The depth to which the ball will sink is (neglect viscous forces) :
A cube of iron whose sides are of length L, is put into mercury. The weight of iron cube is W. The density of iron is rI, that of mercury is rM. The depth to which the cube sinks is given by the expression _
A metal ball of density 7800 kg/m3 is suspected to have a large number of cavities. It weighs 9.8 kg when weighed directly on a balance and 1.5 kg less when immersed in water. The fraction by volume of the cavities in the metal ball is approximately :
A sphere of radius R and made of material of relative density s has a concentric cavity of radius r. It just floats when placed in a tank full of water. The value of the ratio R/r will be
A beaker containing water is placed on the platform of a spring balance. The balance reads 1.5 kg. A stone of mass 0.5 kg and density 500 kg/m3 is immersed in water without touching the walls of beaker. What will be the balance reading now ?
A cylindrical block of area of cross-section A and of material of density r is placed in a liquid of density one-third of density of block. The block compresses a spring and compression in the spring is one-third of the length of the block. If acceleration due to gravity is g, the spring constant of the spring is
A body of density r' is dropped from rest at a height h into a lake of density r, where r > r'. Neglecting all disipative froces, calculate the maximum depth to which the body sinks before returning of float on the surface.
Water is flowing in a horizontal pipe of
non-uniform cross - section. At the most contracted place of the pipe –
Water is flowing in a tube of non-uniform radius. The ratio of the radii at entrance and exit ends of tube is 3 : 2. The ratio of the velocities of water entering in and exiting from the tube will be –
A rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
A jet of water with cross section of 6 cm2 strikes a wall at an angle of 60º to the normal and rebounds elastically from the wall without losing energy. If the velocity of the water in the jet is 12 m/s, the force acting on the wall is
The cross sectional area of a horizontal tube increases along its length linearly, as we move in the direction of flow. The variation of pressure, as we move along its length in the direction of flow (x-direction), is best depicted by which of the following graphs
|
119 videos|494 docs|98 tests
|