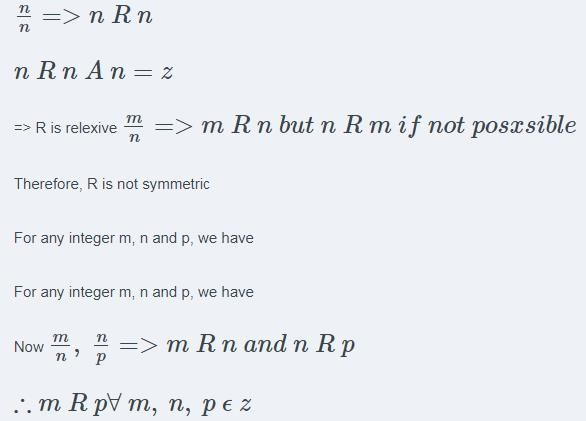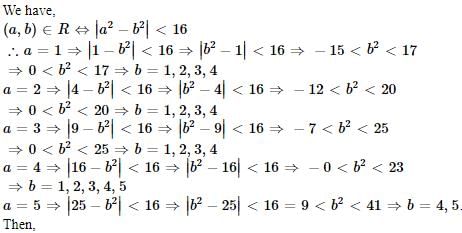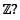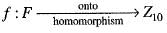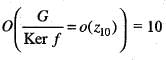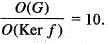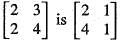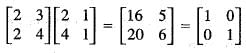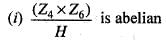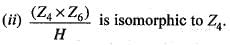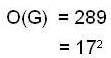Test: Group Theory - 1 - Mathematics MCQ
20 Questions MCQ Test - Test: Group Theory - 1
Consider the following relations, which of the following is an equivalence relation?
Let n be a fixed positive integer. Define a relation R on the set Z of integers by 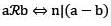 then R is
then R is
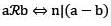 then R is
then R isLet R be a relation over the set 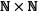 and it is defined by (a, b) R (c, d) ⇔ a + d = b + c then R is
and it is defined by (a, b) R (c, d) ⇔ a + d = b + c then R is
An integer m is said to be related to another integer n if m is a multiple of n then relation is
The number of elements Satisfies g7 = e, g ≠ e in any finite group
The relation R defined on the set A ={1,2,3,4,5} by P = {(x, y) : |x2 —y2| < 16} is given by
Let G be a finite group and Z10 be a homomorphic image of G. Then
The number of all subgroups of the group (Z60, +) of integers modulo 60 is
Let G = { 1, 2,................, p-1} be the group with respect to multiplication modulo p. If the inverse of 110 in G is 4, then p is of the form
Consider the group 2 x 2 non-singular matrices under matrix multiplication over Z5. The inverse of 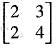 is
is
a, b ε G, a group. If o(a) = 10 and o(b) = 21, then (Where <a> means cyclic group generated by a.)
Consider the following statements:
1. A group of order 289 is abelian.
2. In S3 there are four elements satisfying x2= e and six elements satisfying y3 = e.
3. Every proper subgroup of S3 is cyclic.
4. (Z30, 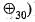 has 4 subgroups of order 15 .
has 4 subgroups of order 15 .
Correct statements are:
Let G be a group order 6, and H be a subgroup of G such that 1 < |H| < 6. Which one of the following options is correct?
If (G, ⋅) is a group such that (ab)-1 = a-1 b-1, ∀ a, b ∈ G, then G is a/an