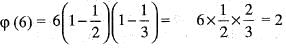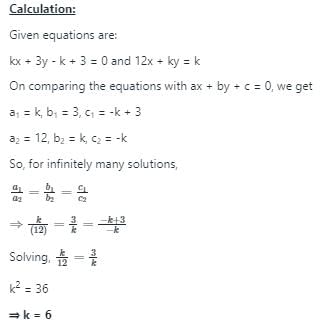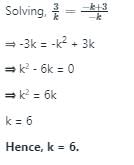Test: Group Theory - 3 - Mathematics MCQ
20 Questions MCQ Test - Test: Group Theory - 3
If N is a set of natural numbers, then under binary operation a · b = a + b, (N, ·) is
The set of all positive rational numbers forms an abelian group under the composition defined by
Set (1,2,3,4} is a finite abelian group of order... under multiplication modulo ... as composition.
Let G be a group of order 7 and φ(x) = x4, x ∈ G. Then f is
If a, b ∈ G, a group, then b is conjugate to a, if there exist c ∈ G, such that
If H1 and H2 are two subgroups of G, then following is also a subgroups of G
If (G, *) is a group and for all a, b ∈ G, b-1 * a-1* b * a = e, then G is
Number of elements of the cyclic group of order 6 can be used as generators of the group are
The multiplicative group {1, -1} is a subgroup of the multiplicative group
A set G with a binary composition denoted multiplicative is a group, if
In the additive group of integers, the order of every elements a ≠ 0 is
Let Z be a set of integers, then under ordinary multiplication (Z, ·) is
Set of all n, nth roots of unity from a finite abelian group of order n with respect to
The generators of a group G = {a, a2, a3, a4, a5, a6 = e) are
If G is a group such that a2 = e, for all a ∈ G, then G is
The value of k for which kx + 3y - k + 3 = 0 and 12x + ky = k have infinite solution is: