All Courses
Get the App Signup / Login
Sign in Open App
Mathematics Exam  >  Mathematics Tests  >  Topic-wise Tests & Solved Examples for Mathematics  >  Test: Group Theory - 4 - Mathematics MCQ

Test: Group Theory - 4 - Mathematics MCQ


Test Description

20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Group Theory - 4

Test: Group Theory - 4 for Mathematics 2025 is part of Topic-wise Tests & Solved Examples for Mathematics preparation. The Test: Group Theory - 4 questions and answers have been prepared according to the Mathematics exam syllabus.The Test: Group Theory - 4 MCQs are made for Mathematics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Group Theory - 4 below.
Solutions of Test: Group Theory - 4 questions in English are available as part of our Topic-wise Tests & Solved Examples for Mathematics for Mathematics & Test: Group Theory - 4 solutions in Hindi for Topic-wise Tests & Solved Examples for Mathematics course. Download more important topics, notes, lectures and mock test series for Mathematics Exam by signing up for free. Attempt Test: Group Theory - 4 | 20 questions in 60 minutes | Mock test for Mathematics preparation | Free important questions MCQ to study Topic-wise Tests & Solved Examples for Mathematics for Mathematics Exam | Download free PDF with solutions
Test: Group Theory - 4 - Question 1
Save

If H is a subgroup of finite group G and order of H and G are respectively, m and n, then

Detailed Solution for Test: Group Theory - 4 - Question 1

  1. Understanding the Problem:
    We are given that H is a subgroup of a finite group G, with |H| = m and |G| = n. We need to determine the relationship between m and n.

  2. Applying Lagrange's Theorem:
    Lagrange's Theorem states:
    If H is a subgroup of a finite group G, then the order of H divides the order of G.
    Symbolically, m | n (i.e., m divides n).

  3. Analyzing the Options:

  • Option A (m | n): Matches Lagrange's Theorem.
  • Option B (n | m): Incorrect, as the order of the group cannot divide the order of its subgroup unless m = n, which is not guaranteed.
  • Option C: No valid claim provided.
  • Option D: Incorrect because Lagrange's Theorem confirms m | n.

Conclusion: The correct answer is A.

Test: Group Theory - 4 - Question 2
Save

Set of rational number of the form m/2n (.m, n integers) is a group under

Detailed Solution for Test: Group Theory - 4 - Question 2

  1. Closure:
    For m/2ⁿ, k/2ⁿ ∈ S, their sum is:
    m/2ⁿ + k/2ⁿ = (m · 2ᶫ + k · 2ⁿ) / 2ⁿ⁺ˡ,
    which retains the form integer/2ⁿ⁺ˡ. Thus, S is closed under addition.

  2. Associativity:
    Addition is associative in Q, so it holds in S.

  3. Identity Element:
    The identity element is 0 = 0/2ⁿ, which belongs to S.

  4. Inverses:
    For any m/2ⁿ ∈ S, its inverse is -m/2ⁿ, which is also in S.

Conclusion:
The set satisfies all group axioms under addition.

Clear all your doubts with EduRev
Test: Group Theory - 4 - Question 3
Save

A necessary and sufficient condition for a non-empty subset H o f a finite group G to be a subgroup is that

Detailed Solution for Test: Group Theory - 4 - Question 3

H is a non-empty complex of a group G. The necessary and sufficient condition for H to be a subgroup of G is: a, b ∈ H ⇒ ab-1 ∈ H, where b-1 is the inverse of b in G.

Test: Group Theory - 4 - Question 4
Save

If G is a finite group and order of group is m, then a ∈ G
Detailed Solution for Test: Group Theory - 4 - Question 4

  1. Lagrange's Theorem:
    In a finite group G of order m, the order (period) of any element a ∈ G divides m. Let k be the order of a, so k | m.

    • This implies m = k · n for some integer n.

  2. Compute aᵐ:
    Since aᵏ = e (by definition of order k),

  3. Verify Options:

    • Option A (aᵐ = e): Correct, as proven above.
    • Option B (aᵐ ≠ e): Incorrect, contradicts Lagrange's Theorem.
    • Option C (aᵐ = a): Implies aᵐ⁻¹ = e, which is not guaranteed.
    • Option D (aᵐ = a⁻¹): Implies aᵐ⁺¹ = e, also not guaranteed.

 

Test: Group Theory - 4 - Question 5
Save

Check the correct statement
Detailed Solution for Test: Group Theory - 4 - Question 5

  1. Statement A:

    • Claim: The identity of a subgroup is the same as that of the group.
    • Verification: By definition, a subgroup H of a group G must share the same identity element e. This is required for closure under the group operation and inverses.
    • Conclusion: Correct

  2. Statement B:

    • Claim: The inverse of any element in the subgroup is the same as its inverse in the group.
    • Verification: In a subgroup H, for any h ∈ H, the inverse h⁻¹ must satisfy h · h⁻¹ = e. Since H inherits the group operation from G, the inverse in H is identical to the inverse in G.
    • Conclusion: Correct 

  3. Statement C:

    • Claim: The order of an element in the subgroup matches its order in the group.
    • Verification: The order of an element h is the smallest positive integer n such that hⁿ = e. This property depends only on the element and the group operation, which are unchanged in the subgroup.
    • Conclusion: Correct 

  4. Statement D (All of the above):

    • Since A, B, and C are all valid, D is the correct choice
Test: Group Theory - 4 - Question 6
Save

In a group G, we have ab = a or ba = a then
Detailed Solution for Test: Group Theory - 4 - Question 6

In a group G, if ab = a or ba = a, then:

Step-by-Step Explanation:

  1. Start with ab = a.

  2. Multiply both sides on the left by a⁻¹:

    Similarly, for ba = a, multiply on the right by a⁻¹.

  3. In both cases, b = e (the identity element).

Answer:

Note: The conclusion b = e holds regardless of the specific element a. The other options are invalid because the given equations do not constrain a or b².

Test: Group Theory - 4 - Question 7
Save

If n is the order of element a of group G, then am = e, an identity element if
Detailed Solution for Test: Group Theory - 4 - Question 7

Uploaded image

Test: Group Theory - 4 - Question 8
Save

Given, a x a = b in G, then x is equal to
Detailed Solution for Test: Group Theory - 4 - Question 8

Given the equation in a group G:

axa = b

  1. Multiply both sides on the left by a⁻¹:
    a⁻¹(axa) = a⁻¹b ⟹ (a⁻¹a)xa = exa = xa = a⁻¹b.

  2. Multiply both sides on the right by a⁻¹:
    xa · a⁻¹ = a⁻¹b · a⁻¹ ⟹ x(aa⁻¹) = xe = x = a⁻¹ba⁻¹.

Test: Group Theory - 4 - Question 9
Save

If H, K are two subgroups of a group G, then H K is a subgroup of G, iff
Detailed Solution for Test: Group Theory - 4 - Question 9

  • Understanding the Product Set HK:
    The product HK = {hk | h in H, k in K}. For HK to be a subgroup of G, it must satisfy closure under the group operation and inverses.

  • Necessity of HK = KH:

    • Closure: If HK = KH, for any h1k1, h2k2 in HK, the product h1k1h2k2 can be rewritten as h1(h2')k1k2, ensuring closure.
    • Inverses: The inverse of hk in HK is k⁻¹h⁻¹. If HK = KH, then k⁻¹h⁻¹ is in HK, so inverses are in HK.

  • Sufficiency of HK = KH:
    If HK is a subgroup, then (hk)⁻¹ = k⁻¹h⁻¹ is in HK. This implies HK is a subset of KH. Similarly, closure under products ensures HK is a subset of KH. Thus, HK = KH.

  • Analysis of Options:

    • A: HK = 1:
      Incorrect. This would require H and K to be trivial, which is not general.
    • B: HK = KH:
      Correct. This is the necessary and sufficient condition for HK to be a subgroup.
    • C: HK = H⁻¹K⁻¹:
      Irrelevant. H⁻¹ = H and K⁻¹ = K for subgroups, so this reduces to HK = HK, which is always true but does not address the subgroup condition.
    • D: None of these:
      Incorrect because B is valid.
Test: Group Theory - 4 - Question 10
Save

The set M of square matrices ( of same order) with respect to matrix multiplication is
Detailed Solution for Test: Group Theory - 4 - Question 10

The set M of square matrices (of same order) with respect to matrix multiplication is a monoid.

A monoid is a set equipped with an associative binary operation and an identity element. In the case of square matrices, the binary operation is matrix multiplication, which is associative. The identity element is the identity matrix, a square matrix with ones on the diagonal and zeros elsewhere.

It is not a group because not every matrix has an inverse (a matrix that, when multiplied by the original matrix, yields the identity matrix).

It is not a quasi-group because although every element has a left and right inverse, these inverses are not necessarily the same.

It is a semi-group because it is a set with an associative binary operation, but this term is less specific than monoid since it doesn't specify the existence of an identity element.

So, the most specific and correct answer is monoid.

Test: Group Theory - 4 - Question 11
Save

In the group G={0,1,2,3,4,5} under addition modulo 6, (2+3−1+4)−1=
Detailed Solution for Test: Group Theory - 4 - Question 11

G is a group under addition modulo 6

0 is the identity

For a,b∈G

If a+b=0, then a−1 = b

Now, 3+3=0 ⟹ 3−1 = 3 ..... (i)

Also, 9+3=12=0 ⟹ 9−1 = 3 ....... (ii)

Consider, (2+3−1+4)−1 

= (2+3+4)−1

= 9−1

= 3
Hence, (2+3−1+4)−1=3

Test: Group Theory - 4 - Question 12
Save

Order of the permutation  is
Detailed Solution for Test: Group Theory - 4 - Question 12

Test: Group Theory - 4 - Question 13
Save

Every finite group G is isomorphic to a permutation group; this statement is
Detailed Solution for Test: Group Theory - 4 - Question 13

  1. Identify Key Terms:
    The question refers to a theorem stating that every finite group G is isomorphic to a permutation group.

  2. Analyze the Options:

    • Lagrange’s Theorem (B): Concerns subgroup orders dividing the group order. Irrelevant here.

    • Liouville’s Theorem (C): Pertains to complex analysis, unrelated to group theory.

    • Cayley’s Theorem (A): States that every group G is isomorphic to a subgroup of the symmetric group Sn​ (permutation group).

    • None of these (D): Incorrect because Cayley’s Theorem directly matches the statement.

  3. Conclusion:
    Cayley’s Theorem confirms the given statement.

Test: Group Theory - 4 - Question 14
Save

The number of elements of S5 (the symmetric group on 5 letters) which are their own inverses equals
Detailed Solution for Test: Group Theory - 4 - Question 14

Le S5 = {a1, a2, a3, a4, a5} be a symmetric group  of order 5. the elements of S5 which are their own inverses are of the type (a1, a2)  or (a1, a2) (a2, a4).

The number of elements of the type (a1, a2) are

The number of elements of the type (a3, a4) are

So the total number of elements which are their own inverses is equal to 25.

pointed that 25 elements of order 2 make 26 self-inverse elements, because the identity is also self-inverse.

Test: Group Theory - 4 - Question 15
Save

If a, b ∈ G, a group of order m, then order of ab and ba are
Detailed Solution for Test: Group Theory - 4 - Question 15

  1. Order of an Element:
    The order of an element g in a group G is the smallest positive integer n such that gⁿ = e, where e is the identity.

  2. Relationship Between ab and ba:

    • Observe that ab and ba are conjugate elements. Specifically, ba = a⁻¹(ab)a, so ba is conjugate to ab.
    • Key Property: Conjugate elements have the same order.

  3. Proof Using Powers:

    • Suppose (ab)ⁿ = e. Then:
      (ba)ⁿ = b(ab)ⁿ⁻¹a = b · e · a = ba (if n = 1).
    • For general n, use induction or note that (ba)ⁿ = a⁻¹(ab)ⁿa. If (ab)ⁿ = e, then (ba)ⁿ = a⁻¹ea = e.
    • Similarly, if (ba)ⁿ = e, then (ab)ⁿ = e.
    • Thus, the smallest n satisfying (ab)ⁿ = e equals the smallest n for (ba)ⁿ = e.

  4. Examples in Non-Abelian Groups:

    • In S₃, let a = (1 2 3) and b = (1 2). Then ab = (1 3) (order 2) and ba = (2 3) (order 2).
    • Another example: a = (1 2), b = (2 3). Then ab = (1 2 3) (order 3) and ba = (1 3 2) (order 3).

Conclusion:
The order of ab and ba are always the same in any group G.

Test: Group Theory - 4 - Question 16
Save

The set of all non-singular square matrices of same order with respect to matrix multiplication is
Detailed Solution for Test: Group Theory - 4 - Question 16

  1. Identify the Algebraic Structure:

    • The set in question is all non-singular (invertible) square matrices of the same order under matrix multiplication.

    • Non-singular matrices have multiplicative inverses by definition.

  2. Check Group Axioms:

    • Closure: The product of two invertible matrices is invertible.

    • Associativity: Matrix multiplication is associative.

    • Identity Element: The identity matrix II serves as the multiplicative identity.

    • Inverses: Every non-singular matrix has an inverse.

    Since all group axioms are satisfied, the set forms a group.

  3. Eliminate Incorrect Options:

    • A (Quasi-group): A group is a quasi-group, but this is not the most specific answer.

    • B (Monoid): A monoid lacks inverses for all elements; here, inverses exist.

    • D (Abelian Group): Matrix multiplication is not commutative in general, so the group is non-abelian.

  4. Hence option C is correct

Test: Group Theory - 4 - Question 17
Save

Two permutation f and g of degree n are said to be equal, if we have
Detailed Solution for Test: Group Theory - 4 - Question 17
  • Permutations are bijective functions that rearrange elements of a set S. Two functions are equal if they produce the same output for every input in S.

Analysis of Options:

  • A: f(a) + g(a) = 1 for all a in S
    This implies arithmetic operations on permutations, which are not part of their definition. Irrelevant for equality. False.
  • B: f(a) - g(a) = 1 for all a in S
    Similar to A, subtraction of permutations is undefined in the context of equality. False.
  • C: f(a) = g(a) for all a in S
    Matches the standard definition of equality for functions: identical mappings for all inputs. True.
  • D: None of these
    Invalid since C is correct.

Conclusion:
Two permutations are equal if they map every element a in S to the same position. The correct answer is: C.

Test: Group Theory - 4 - Question 18
Save

If 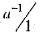 and 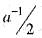are two multiplicative inverse of non-zero elements a ∈ F, a field, than
Detailed Solution for Test: Group Theory - 4 - Question 18

Test: Group Theory - 4 - Question 19
Save

If G is a finite group of order n, a ∈ G and order of a is m 7M, if G is cylic, then
Detailed Solution for Test: Group Theory - 4 - Question 19

In a finite cyclic group G, the order of the group G is n, and every element a in G has an order m. If G is cyclic, there exists an element g in G (called a generator) such that every other element in G can be written as powers of g.

  • The order of a cyclic group is the same as the order of the generator. So if G is cyclic and has order n, then the generator g must have order n.
  • For any element a in G, if a = gk, the order of a (denoted m) is such that am = e, where e is the identity element of G. In a cyclic group, the order of any element divides the order of the group. Therefore, the order m of any element a must be a divisor of n.
  • For a to generate the whole group G, the order of a must be equal to the order of the group n. Hence, m = n when a is a generator.

Thus, in a cyclic group, the order m of any element a is equal to the order of the group n when the element generates the entire group. Therefore, the answer is A: m = n.

Test: Group Theory - 4 - Question 20
Save

If a is an element of order n of group G and p is prime to n, then order of ap is 
Detailed Solution for Test: Group Theory - 4 - Question 20

27 docs|150 tests
Join Course
Information about Test: Group Theory - 4 Page
In this test you can find the Exam questions for Test: Group Theory - 4 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Group Theory - 4, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for Group Theory - 4

Find all the important questions for Group Theory - 4 at EduRev.Get fully prepared for Group Theory - 4 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Group Theory - 4 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Group Theory - 4 resources.

Group Theory - 4 MCQs with Answers

Prepare for the Group Theory - 4 within the Mathematics exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Group Theory - 4 Topic-wise Tests & Solved Examples for Mathematics

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Group Theory - 4 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup