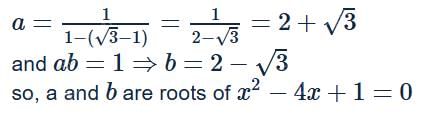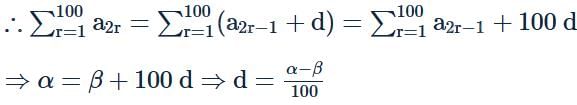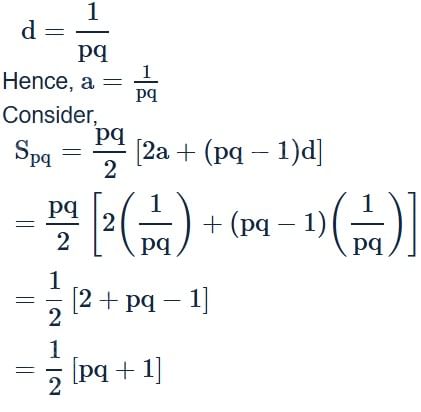Test: Introduction To Sequences - JEE MCQ
10 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Introduction To Sequences
The first 4 terms of the sequence a1 = 2, an = 2an-1 + 1 for n > 2 are
What is the 10th term of the sequence defined by an = (n-1)(2-n)(3+n)?
If |3x−1|,3,|x−3| are the first three terms of an arithmetic progression, then the sum of the first five terms can be
Consider the sequence 8 A + 2 B,6 A + B,4 A 2 A−B,……., Which term of this sequence will have a coefficient of A which is twice the coefficient of B?
If a = 1 +(√3 − 1) + (√3 − 1)2 + (√3 − 1)3 + .... and ab = 1, then a and b are the roots of the equation
7th term of Geometric Progression 2, 6, 18, ... is
Let an be the nth term of an A.P. If 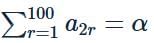 and
and 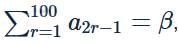 then the common difference of the A.P. is
then the common difference of the A.P. is
If the pth term of an A.P. be 1/q and qth term be 1/p, then the sum of its pqth terms will be
If a, b, c are in A. P., then (a + 2b − c)(2b + c − a)(c + a − b) equals
|
176 videos|588 docs|160 tests
|
|
176 videos|588 docs|160 tests
|